题目内容
18.一条直线过点P(3,2),倾斜角是直线y=$\sqrt{3}$x+3的倾斜角的2倍,求这条直线的方程.分析 由已知直线的方程求出其倾斜角的正切值,利用二倍角的正确求得所求直线的斜率,代入直线方程的点斜式得答案.
解答 解:设直线y=$\sqrt{3}$x+3的倾斜角为α,则tanα=$\sqrt{3}$.
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}=\frac{2\sqrt{3}}{1-(\sqrt{3})^{2}}=-\sqrt{3}$.
即所求直线的斜率为$-\sqrt{3}$.
由直线方程的点斜式得所求直线方程为y-2=$-\sqrt{3}(x-3)$.
整理得:$\sqrt{3}x+y-2-3\sqrt{3}=0$.
点评 本题考查直线的倾斜角,考查了直线的斜率,训练了倍角公式的应用,是基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
6.在等差数列{an}中,若a1=3,公差d≠0,则$\lim_{n→∞}$$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{{a}_{2}+{a}_{4}+…+{a}_{2n}}$的值( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 0 |
9.已知函数f(2x)=log3(x-2)+|1-x|,则f(6)=( )
| A. | 2 | B. | 3 | C. | 5 | D. | 8 |
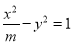 的实轴长是离心率的2倍,则m= .
的实轴长是离心率的2倍,则m= .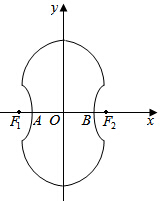 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.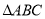 的外接圆为
的外接圆为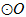 ,延长
,延长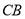 至
至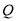 ,再延长
,再延长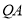 至
至 ,使得
,使得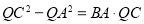 .
.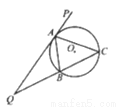
 的切线;
的切线;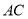 恰好为
恰好为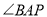 的平分线,
的平分线,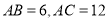 ,求
,求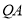 的长度.
的长度. 且
且 是单调增函数;命题
是单调增函数;命题 ,
, .则下列命题为真命题的是( )
.则下列命题为真命题的是( ) B.
B. C.
C. D.
D.