题目内容
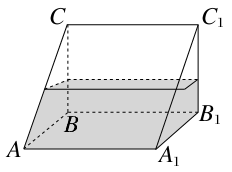
一个空间几何体的三视图如图所示，则该几何体的的体积为
A． |
B． |
C． |
D． |
C
解析考点：由三视图求面积、体积．
分析：由三视图可以看出，此几何体是一个上部为圆锥、下部为圆柱的几何体，故可以分部分求出圆锥与圆柱的体积再相加求出此简单组合体的体积．
解：所求几何体为一个圆柱体和圆锥体构成．
其中圆锥的高为
=
．其体积为
π?12?=
π
圆柱的体积为π?12?2=2π
故此简单组合体的体积V=π+2π
故选C．
练习册系列答案
相关题目
的图象绕
轴旋转一周所形成的几何体的体积为__________.一个几何体的三视图如图，该几何体的表面积为
| A．280 | B．292 | C．360 | D．372 |
用与球心距离为1的平面去截球，所得的截面面积为π，则球的休积为
A． | B． | C． | D． |
，在该几何体的正视图中，这条棱的投影是长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为
和
的线段，则
的最大值为（ ）
一简单组合体的三视图及尺寸如右图所示（单位: 
）则该组合体的体积为（ ）
| A．60000 | B．64000 | C．70000 | D．72000 |
