题目内容
15．下列函数中，在区间（0，+∞）上为增函数的是（ ）| A． | y=|x-1| | B． | y=-x2 | C． | $y=\sqrt{x+1}$ | D． | y=2-x |
分析 分别判断函数的单调性即可得到结论．
解答 解：对于A，y=|x-1|=$\left\{\begin{array}{l}{x-1，x＞1}\\{-x+1，x≤1}\end{array}\right.$，函数在（1，+∞）为增函数，
对于B，y=-x2在（0，+∞）为减函数，
对于C，y=$\sqrt{x+1}$在[-1，+∞）为增函数，故在（0，+∞）为增函数，
对于D，y=2-x在R上为减函数，
故选：C．
点评 本题主要考查函数单调性的判断，要求熟练掌握常见函数单调性的性质．
练习册系列答案
相关题目
5．圆（x-1）2+（y+2）2=6与直线2x+y-5=0的位置关系是（ ）
| A． | 相切 | B． | 相交但直线不过圆心 | ||
| C． | 相交且过圆心 | D． | 相离 |
3．若函数f（x）=sin（ωx+θ）的图象（部分）如图所示，则ω和θ的取值是（ ）
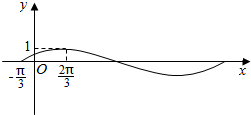
| A． | $ω=1，θ=\frac{π}{3}$ | B． | $ω=1，θ=-\frac{π}{3}$ | C． | $ω=\frac{1}{2}，θ=\frac{π}{6}$ | D． | $ω=\frac{1}{2}，θ=-\frac{π}{6}$ |
10．下列计算错误的是（ ）
| A． | ${∫}_{-π}^{π}sinxdx=0$ | B． | $\int_{-\frac{π}{2}}^{\frac{π}{2}}{cos2xdx=\frac{1}{2}}$ | ||
| C． | ${∫}_{-\frac{π}{2}}^{\frac{π}{2}}cosxdx={2∫}_{0}^{\frac{π}{2}}cosxdx$ | D． | ${∫}_{0}^{1}\sqrt{x}dx=\frac{2}{3}$ |
4．若f（x）=x3-ax+1在（0，1）上单调递减，则实数a的取值范围是（ ）
| A． | a≤2 | B． | a≤3 | C． | a＞3 | D． | a≥3 |