题目内容
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数.
(1)求b的值,并求a的取值范围;
(2)判断f(x)在其定义域R上的零点的个数.
解:(1)由已知得f′(x)=-3x2+2ax+b…(1分),
因为f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
所以f(x)在x=0处取得极小值,f′(0)=0…(2分),解得b=0…(3分),
又因为f(x)在(0,1)上是增函数,所以f′(x)=-3x2+2ax>0,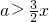 …(4分),
…(4分),
当x∈(0,1)时,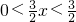 ,所以a的取值范围是
,所以a的取值范围是 …(5分),
…(5分),
(2)由(1)得 ,解f′(x)=0得x=0或
,解f′(x)=0得x=0或 …(6分),
…(6分),
…(9分)
(i)①当f(0)=c>0时,由上表知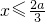 ,f(x)>0,x取某个充分大的实数(例如
,f(x)>0,x取某个充分大的实数(例如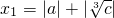 )时,f(x1)<0,f(x)在定义域上连续,所以f(x)在区间
)时,f(x1)<0,f(x)在定义域上连续,所以f(x)在区间 上有一个零点,从而f(x)在其定义域R上有1个零点…(10分);
上有一个零点,从而f(x)在其定义域R上有1个零点…(10分);
②当f(0)=c=0时,f(x)在区间 上有一个零点,从而f(x)在其定义域R上有2个零点…(11分);
上有一个零点,从而f(x)在其定义域R上有2个零点…(11分);
③当f(0)=c<0时,(ⅰ)若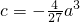 ,则
,则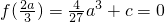 ,x取某个充分小的实数(例如x2=-|a|)时,f(x2)>0,所以f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有2个零点…(12分);
,x取某个充分小的实数(例如x2=-|a|)时,f(x2)>0,所以f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有2个零点…(12分);
(ⅱ)若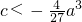 ,则
,则 时,由上表知?x≥0,f(x)<0,f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有1个零点…(13分);
时,由上表知?x≥0,f(x)<0,f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有1个零点…(13分);
(ⅲ)若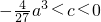 ,则
,则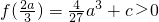 时,f(x)在区间(x2,0)、
时,f(x)在区间(x2,0)、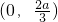 、
、 上各有一个零点,从而f(x)在其定义域R上有3个零点…(14分);
上各有一个零点,从而f(x)在其定义域R上有3个零点…(14分);
综上所述,当c>0或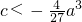 时,f(x)在其定义域R上有1个零点;当c=0或
时,f(x)在其定义域R上有1个零点;当c=0或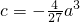 时,f(x)在其定义域R上有2个零点;当
时,f(x)在其定义域R上有2个零点;当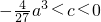 时,f(x)在其定义域R上有3个零点.
时,f(x)在其定义域R上有3个零点.
分析:(1)求出导函数,据已知条件中函数的单调性,判断出x=0是一个极值点,将x=0代入导函数得到函数值为0,求出b的值.将b的值代入f(x)中,利用f(x)在(0,1)上是增函数,判断出f′(x)=-3x2+2ax>0在(0,1)上恒成立,列出不等式求出a的范围.
(2)利用函数在定义域内的单调性和最值研究零点的个数,对f(x)求导,找到单调区间,确定极值点,最后对极值点进行分类讨论则得到零点个数.
点评:本题主要考查导数为0时取到函数的极值的问题、根的存在性及根的个数判断.这里多注意分类讨论的思想.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,也是教学中的重点和难点,学生应熟练掌握.
因为f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
所以f(x)在x=0处取得极小值,f′(0)=0…(2分),解得b=0…(3分),
又因为f(x)在(0,1)上是增函数,所以f′(x)=-3x2+2ax>0,
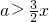 …(4分),
…(4分),当x∈(0,1)时,
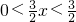 ,所以a的取值范围是
,所以a的取值范围是 …(5分),
…(5分),(2)由(1)得
 ,解f′(x)=0得x=0或
,解f′(x)=0得x=0或 …(6分),
…(6分),| x | (-∞,0) | 0 | 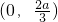 |  | 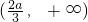 |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
(i)①当f(0)=c>0时,由上表知
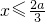 ,f(x)>0,x取某个充分大的实数(例如
,f(x)>0,x取某个充分大的实数(例如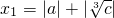 )时,f(x1)<0,f(x)在定义域上连续,所以f(x)在区间
)时,f(x1)<0,f(x)在定义域上连续,所以f(x)在区间 上有一个零点,从而f(x)在其定义域R上有1个零点…(10分);
上有一个零点,从而f(x)在其定义域R上有1个零点…(10分);②当f(0)=c=0时,f(x)在区间
 上有一个零点,从而f(x)在其定义域R上有2个零点…(11分);
上有一个零点,从而f(x)在其定义域R上有2个零点…(11分);③当f(0)=c<0时,(ⅰ)若
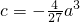 ,则
,则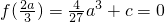 ,x取某个充分小的实数(例如x2=-|a|)时,f(x2)>0,所以f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有2个零点…(12分);
,x取某个充分小的实数(例如x2=-|a|)时,f(x2)>0,所以f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有2个零点…(12分);(ⅱ)若
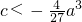 ,则
,则 时,由上表知?x≥0,f(x)<0,f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有1个零点…(13分);
时,由上表知?x≥0,f(x)<0,f(x)在区间(x2,0)上有一个零点,从而f(x)在其定义域R上有1个零点…(13分);(ⅲ)若
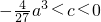 ,则
,则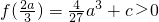 时,f(x)在区间(x2,0)、
时,f(x)在区间(x2,0)、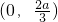 、
、 上各有一个零点,从而f(x)在其定义域R上有3个零点…(14分);
上各有一个零点,从而f(x)在其定义域R上有3个零点…(14分);综上所述,当c>0或
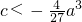 时,f(x)在其定义域R上有1个零点;当c=0或
时,f(x)在其定义域R上有1个零点;当c=0或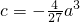 时,f(x)在其定义域R上有2个零点;当
时,f(x)在其定义域R上有2个零点;当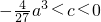 时,f(x)在其定义域R上有3个零点.
时,f(x)在其定义域R上有3个零点.分析:(1)求出导函数,据已知条件中函数的单调性,判断出x=0是一个极值点,将x=0代入导函数得到函数值为0,求出b的值.将b的值代入f(x)中,利用f(x)在(0,1)上是增函数,判断出f′(x)=-3x2+2ax>0在(0,1)上恒成立,列出不等式求出a的范围.
(2)利用函数在定义域内的单调性和最值研究零点的个数,对f(x)求导,找到单调区间,确定极值点,最后对极值点进行分类讨论则得到零点个数.
点评:本题主要考查导数为0时取到函数的极值的问题、根的存在性及根的个数判断.这里多注意分类讨论的思想.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,也是教学中的重点和难点,学生应熟练掌握.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|