题目内容
已知函数f(x)=3x-x2,问:方程f(x)=0在区间[-1,0]内有没有实数解?为什么?
解:因为f(-1)=3-1-(-1)2=-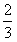 <0,f(0)=30-02=1>0,
<0,f(0)=30-02=1>0,
又函数f(x)=3x-x2的图象是连续曲线,
所以f(x)在区间[-1,0]内有零点,即f(x)=0在区间[-1,0]内有实数解。
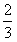 <0,f(0)=30-02=1>0,
<0,f(0)=30-02=1>0,又函数f(x)=3x-x2的图象是连续曲线,
所以f(x)在区间[-1,0]内有零点,即f(x)=0在区间[-1,0]内有实数解。

练习册系列答案
相关题目