题目内容
如图,在底角为 的等腰梯形
的等腰梯形 中,已知
中,已知 ,
, 分别为
分别为 ,
, 的中点.设
的中点.设 ,
, .
.
(1)试用 ,
, 表示
表示 ,
, ;
;
(2)若 ,试求
,试求 的值.
的值.
(1) ,
, ; (2)
; (2) .
.
解析试题分析:(1) 利用平面向量的加法和减法的运算法则进行计算,用已知量表示未知量,注意向量的方向的变化;(2)要求 ,就要找到向量
,就要找到向量 ,
, 的模及其数量积,先求出向量
的模及其数量积,先求出向量 的模,再根据向量的性质进行计算.
的模,再根据向量的性质进行计算.
试题解析:(1)因为 ,
, ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点,
所以 ; 3分
; 3分 . 6分
. 6分
(2) ,
, ,
,  ,所以
,所以 , 8分
, 8分
那么 . 12分
. 12分
考点:1、平面向量的模及数量积;2、平面向量的加减混合运算.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知平面向量 ,
, ,且
,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
若向量 ,满足条件
,满足条件 ,则x=( )
,则x=( )
| A.6 | B.5 | C.4 | D.3 |
 ABC中,G为中线AM为中点,O为
ABC中,G为中线AM为中点,O为 ,
, ,
, ,求
,求 (用
(用 、
、 、
、 表示)
表示)
 .
. 及
及 ;
; 与
与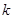 的值.
的值. 中,已知
中,已知 ,
, 的延长线上存在点
的延长线上存在点 ,使
,使 ,求
,求 且
且 ∥
∥ ,则
,则 =
=