题目内容
(本题满分14分)设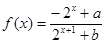 (
(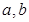 为实常数).
为实常数).
(1)当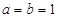 时,证明:
时,证明: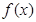 不是奇函数;
不是奇函数;
(2)设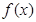 是奇函数,求
是奇函数,求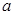 与
与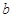 的值;
的值;
(3)当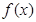 是奇函数时,证明对任何实数
是奇函数时,证明对任何实数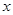 、c都有
、c都有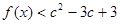 成立
成立
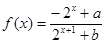 (
(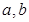 为实常数).
为实常数).(1)当
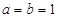 时,证明:
时,证明: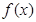 不是奇函数;
不是奇函数;(2)设
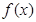 是奇函数,求
是奇函数,求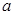 与
与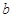 的值;
的值;(3)当
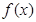 是奇函数时,证明对任何实数
是奇函数时,证明对任何实数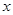 、c都有
、c都有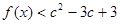 成立
成立 (1)见解析; (2)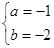 (舍)或
(舍)或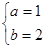 .(3)见解析。
.(3)见解析。
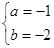 (舍)或
(舍)或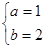 .(3)见解析。
.(3)见解析。本试题主要是考查了函数奇偶性和单调性的证明。
(1) 根据已知条件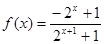 ,
,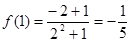 ,
,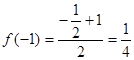 ,所以
,所以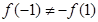 ,
,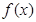 不是奇函数;
不是奇函数;
(2)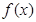 是奇函数时,
是奇函数时,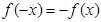 ,即
,即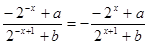 对任意实数
对任意实数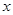 成立.化简整理得
成立.化简整理得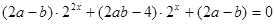 ,这是关于
,这是关于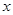 的恒等式,求解参数a,b的范围。
的恒等式,求解参数a,b的范围。
(3)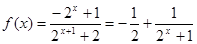 ,因为
,因为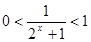 ,得到参数的范围。
,得到参数的范围。
解(1)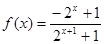 ,
,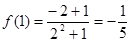 ,
,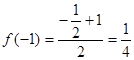 ,所以
,所以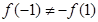 ,
,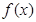 不是奇函数;
不是奇函数;
(2)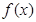 是奇函数时,
是奇函数时,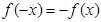 ,即
,即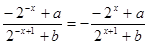 对任意实数
对任意实数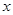 成立.化简整理得
成立.化简整理得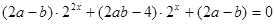 ,这是关于
,这是关于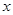 的恒等式,所以
的恒等式,所以
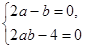 所以
所以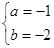 (舍)或
(舍)或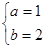 .
.
(3)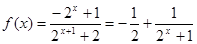 ,因为
,因为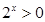 ,所以
,所以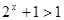 ,
,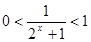 ,从而
,从而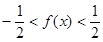 ;而
;而 对任何实数
对任何实数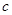 成立,所以对任何实数
成立,所以对任何实数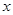 、c都有
、c都有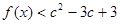 成立.
成立.
(1) 根据已知条件
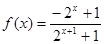 ,
,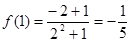 ,
,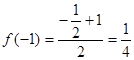 ,所以
,所以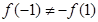 ,
,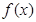 不是奇函数;
不是奇函数;(2)
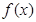 是奇函数时,
是奇函数时,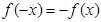 ,即
,即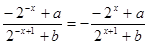 对任意实数
对任意实数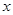 成立.化简整理得
成立.化简整理得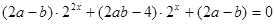 ,这是关于
,这是关于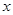 的恒等式,求解参数a,b的范围。
的恒等式,求解参数a,b的范围。(3)
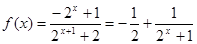 ,因为
,因为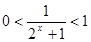 ,得到参数的范围。
,得到参数的范围。解(1)
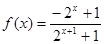 ,
,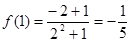 ,
,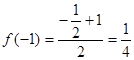 ,所以
,所以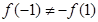 ,
,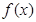 不是奇函数;
不是奇函数; (2)
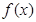 是奇函数时,
是奇函数时,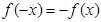 ,即
,即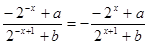 对任意实数
对任意实数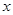 成立.化简整理得
成立.化简整理得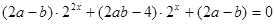 ,这是关于
,这是关于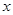 的恒等式,所以
的恒等式,所以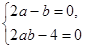 所以
所以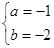 (舍)或
(舍)或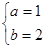 .
.(3)
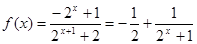 ,因为
,因为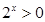 ,所以
,所以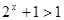 ,
,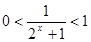 ,从而
,从而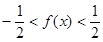 ;而
;而 对任何实数
对任何实数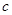 成立,所以对任何实数
成立,所以对任何实数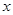 、c都有
、c都有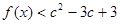 成立.
成立. 
练习册系列答案
相关题目
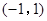 上的函数
上的函数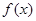 满足
满足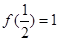 ,且对任意
,且对任意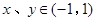 有
有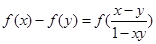 .
.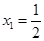 ,
,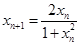 ,求数列
,求数列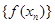 的通项公式.
的通项公式.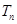 为
为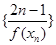 的前
的前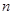 项和,若
项和,若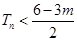 对
对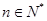 恒成立,求
恒成立,求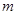 的最大值.
的最大值.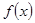 在
在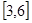 上为增函数,在
上为增函数,在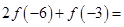 ____________;
____________;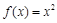
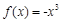
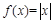
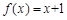
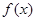 满足
满足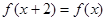 ,且当
,且当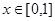 时,
时,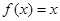 ,则函数
,则函数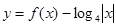 的零点的个数为( )
的零点的个数为( )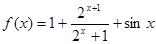 在区间
在区间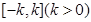 上的值域为
上的值域为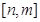 ,则
,则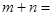 ( )
( )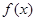 是奇函数,当
是奇函数,当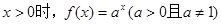 ,且
,且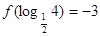 ,
,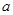 的值为( )
的值为( )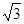
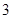
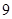
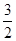
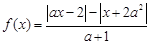 为奇函数,则实数a = .
为奇函数,则实数a = . 是奇函数,且当
是奇函数,且当 时,
时,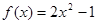 ,那么
,那么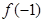 =_______________.
=_______________.