题目内容
(12分)函数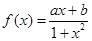 是定义域在(-1,1)上奇函数,且
是定义域在(-1,1)上奇函数,且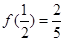 .
.
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)解不等式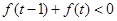 .
.
(1) (2)
(2) 
解析
即

(2)证明:任取 ,
,
则 =
= .
.
∵ ,∴
,∴
 ∴
∴
∴ 在(-1,1)上是增函数.
在(-1,1)上是增函数.
(3)
∵ 在(-1,1)上是增函数
在(-1,1)上是增函数
∴ ,解得
,解得 .
.
考点:本题考察奇函数的定义、函数的单调性以及单调性的应用。
点评:(1)单调性的证明过程中注意一定要化为能够清楚判断正负的乘积形式(2)应用单调性解不等式注意函数的定义域。

练习册系列答案
相关题目
 定义在R上的偶函数,当
定义在R上的偶函数,当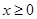 时,
时,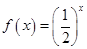
 的函数
的函数 同时满足:
同时满足: ,总有
,总有 ; ②
; ② ;
; ,则有
,则有 成立。
成立。 的值;
的值; ,总有
,总有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。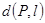 。
。 ,线段
,线段 ,求
,求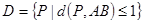 所表示图形的面积;
所表示图形的面积; 所表示的图形。(本题满分14分)
所表示的图形。(本题满分14分)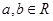 ,且
,且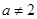 ,定义在区间
,定义在区间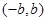 内的函数
内的函数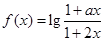 是奇函数.
是奇函数.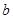 的取值范围;
的取值范围; 的单调性并证明.
的单调性并证明. 是R上的偶函数,且当
是R上的偶函数,且当 时,函数解析式为
时,函数解析式为 ,
, 的值;
的值; 时,函数的解析式。
时,函数的解析式。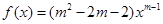 为偶函数,且在区间
为偶函数,且在区间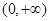 上是单调递减函数,
上是单调递减函数, 的解析式;
的解析式;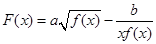 的奇偶性。 (12分)
的奇偶性。 (12分) 在
在 上的单调性.
上的单调性. (单位:万元)随销售利润
(单位:万元)随销售利润 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的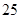 %.现有三个奖励模型:
%.现有三个奖励模型: ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: )
)