题目内容
已知等差数列{an}中,公差d>0,其前n项和为Sn,且满足a2·a3=45,a1+a4=14.
(1)求数列{an}的通项公式;
(2)设由bn=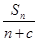 (c≠0)构成的新数列为{bn},求证:当且仅当c=-
(c≠0)构成的新数列为{bn},求证:当且仅当c=-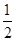 时,数列{bn}是等差数列.
时,数列{bn}是等差数列.
(1)求数列{an}的通项公式;
(2)设由bn=
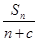 (c≠0)构成的新数列为{bn},求证:当且仅当c=-
(c≠0)构成的新数列为{bn},求证:当且仅当c=-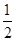 时,数列{bn}是等差数列.
时,数列{bn}是等差数列.(1)an=4n-3.(2)见解析
(1)解:∵等差数列{an}中,公差d>0,
∴ ?d=4故an=4n-3.
?d=4故an=4n-3.
(2)证明:Sn= =n(2n-1),bn=
=n(2n-1),bn=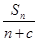 =
= .由2b2=b1+b3,得
.由2b2=b1+b3,得
 ,
,
化简得2c2+c=0,c≠0,∴c=-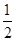 .
.
反之,令c=-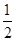 ,即得bn=2n,显然数列{bn}为等差数列,
,即得bn=2n,显然数列{bn}为等差数列,
∴当且仅当c=-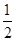 时,数列{bn}为等差数列
时,数列{bn}为等差数列
∴
 ?d=4故an=4n-3.
?d=4故an=4n-3.(2)证明:Sn=
 =n(2n-1),bn=
=n(2n-1),bn=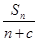 =
= .由2b2=b1+b3,得
.由2b2=b1+b3,得 ,
,化简得2c2+c=0,c≠0,∴c=-
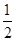 .
.反之,令c=-
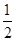 ,即得bn=2n,显然数列{bn}为等差数列,
,即得bn=2n,显然数列{bn}为等差数列,∴当且仅当c=-
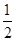 时,数列{bn}为等差数列
时,数列{bn}为等差数列
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).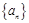 的前
的前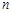 项和为
项和为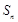 ,若
,若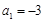 ,
,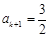 ,
,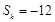 ,则正整数
,则正整数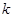 = .
= .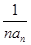 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.