题目内容
18.$\frac{(2sin20°-cos10°)}{sin10°}$+$\frac{sin50°(1+\sqrt{3}tan10°)-cos20°}{cos80°\sqrt{1-cos20°}}$=$\sqrt{2}-\sqrt{3}$.分析 利用二倍角公式以及同角三角函数的基本关系式,化简求解即可.
解答 解:$\frac{(2sin20°-cos10°)}{sin10°}$+$\frac{sin50°(1+\sqrt{3}tan10°)-cos20°}{cos80°\sqrt{1-cos20°}}$
=$\frac{2sin(30°-10°)-cos10°}{sin10°}$+$\frac{sin50°(1+\sqrt{3}\frac{sin10°}{cos10°})-cos20°}{\sqrt{2}sin10°sin10°}$
=$\frac{cos10°-\sqrt{3}sin10°-cos10°}{sin10°}$+$\frac{\frac{2sin50°sin40°}{cos10°}-cos20°}{\sqrt{2}sin10°sin10°}$
=-$\sqrt{3}$+$\frac{\frac{cos10°}{cos10°}-cos20°}{\sqrt{2}sin10°sin10°}$
=-$\sqrt{3}$+$\frac{1-cos20°}{\sqrt{2}sin10°sin10°}$
=-$\sqrt{3}$+$\frac{1-1+2{sin}^{2}10°}{\sqrt{2}sin10°sin10°}$
=-$\sqrt{3}+$$\sqrt{2}$
=$\sqrt{2}-\sqrt{3}$.
点评 本题考查两角和与差的三角函数,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.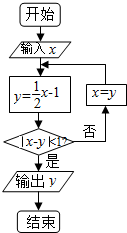 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )| A. | 1 | B. | $-\frac{1}{2}$ | C. | $-\frac{5}{4}$ | D. | $-\frac{13}{8}$ |
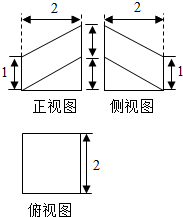 某几何体的三视图如图所示,求该几何体的体积.
某几何体的三视图如图所示,求该几何体的体积.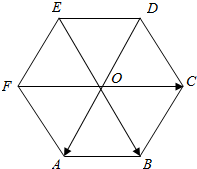 如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.
如图所示.O是正六边形ABCDEF的中心,且$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$.