题目内容

设数列{an}是公差不为零的等差数列，Sn是数列｛an｝的前n项和，且S32=9S2,S4=4S2,求数列｛an｝的通项公式.

解析：∵｛an｝是一个等差数列且公差d≠0,?

∴由S3＝3a2,S2=a1+a2且S32=9(a1+a2)，可知?

9a22=9a1+9a2，即a22=a1+a2.             ①?

又S4=4S2,?

∴a1+a2+a3+a4=4(a1+a2).?

∴a3+a4=3(a1+a2).                              ②?

 

 

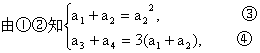
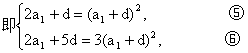
∴6a1+3d=2a1+5d,即2a1=d.⑦?

⑦代入⑤中有4a1=(3a1)2,?

∴a1(9a1-4)=0.?

∵d≠0,可知a1≠0,

∴9a1-4=0.?

∴a1=.∴d=.?

∴an=+(n-1)·.?

∴an=n-.


练习册系列答案
相关题目
设数列{an}是公差不为0的等差数列，Sn为前n项和，满足a3，2a5，a12成等差数列，S10=60．
（1）求数列{an}的通项公式及前n项和Sn；
（2）试求|a1|+|a2|+|a3|+…+|an|．
设数列{an}是公差不为0的等差数列，a1=1且a1，a3，a6成等比数列，则{an}的前n项和Sn等于（　　）
（2012•德州一模）设数列{an}是公差不为0的等差数列，a1=1且a1，a3，a6成等比数列，则数列{an}的前n项和Sn=
1
8
n2+
7
8
n
1
8
n2+
7
8
n
．
（2013•南京二模）设数列{an}是公差不为0的等差数列，Sn为其前n项和，若
a
2
1
+
a
2
2
=
a
2
3
+
a
2
4
，S5=5，则a7的值为
9
9
．
设数列{an}是公差不为0的等差数列，Sn为前n项和，满足a3，2a5，a12 成等差数列，S10=60．
（1）求数列{an}的通项公式及前n项和Sn；
（2）试求所有正整数m，使
am+12+2am
为数列{an}中的项．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网