题目内容
已知函数f(x)＝－x2＋2ax＋1－a在x∈[0,1]时有最大值2，求a的值．
a=2，或a=-1
试题分析：因为函数f(x)＝－x2＋2ax＋1－a在x∈[0,1]时有最大值2，通过配方可知函数的对称轴为x=a,且知该二次函数的开口向下，按
、
、
分类讨论，结合图象就可用a将函数在[0,1]的最大值表示出来，再令其等于2就可解得a值．试题解析：由f(x)＝－x2＋2ax＋1－a＝
知其对称轴为：
，又因为x∈[0,1]；（1）当
时，函数
在[0，1]上是减函数，所以
；（2）当
时，函数在[0，1]上是增函数，所以
；（3）当
时，函数在[0，1]上的最大值为
故舍去．综上可知：a=2，或a=-1
练习册系列答案
相关题目
，
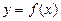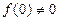，当x＞0时，
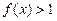，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.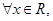
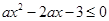恒成立”是真命题，则实数a的取值范围是 .
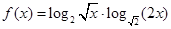的最小值为_________.
+
.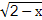