题目内容
(本小题满分12分)
如图,棱柱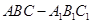 的侧面
的侧面 是菱形,
是菱形,

(1)证明:平面
 平面
平面 ;
;
(2)设 是
是 上的点,且
上的点,且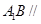 平面
平面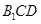 ,求
,求 的值.
的值.
【答案】
(1)根据三棱柱的性质可知 平面
平面 ,然后结合面面垂直的判定定理得到结论。
,然后结合面面垂直的判定定理得到结论。
(2)
【解析】
试题分析:解:

(1)因为侧面 是菱形,所以
是菱形,所以
又已知
所又 平面
平面 ,又
,又 平面
平面 ,
,
所以平面 平面
平面
(2)设 交
交 于点
于点 ,连结
,连结 ,
,
则 是平面
是平面 与平面
与平面 的交线,
的交线,
因为 //平面
//平面 ,所以
,所以 //
// .
.
又 是
是 的中点,所以
的中点,所以 为
为 的中点.
的中点.
即 .
.
考点:本试题考查了面面垂直以及线面平行的性质定理的运用。
点评:对于空间中的面面位置关系,以及线面位置关系的判定,结合相似比来求解结论,属于解题的关键,考查分析问题和解决问题,以及转化思想的运用。属于基础题。

练习册系列答案
相关题目