题目内容
已知离心率为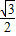 的椭圆
的椭圆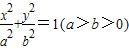 上的点到左焦点F的最长距离为
上的点到左焦点F的最长距离为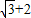 .
.(1)求椭圆的方程;
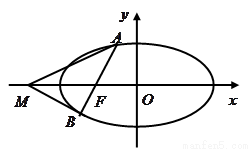
(2)如图,过椭圆的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”,求椭圆的“左特征点”M的坐标.
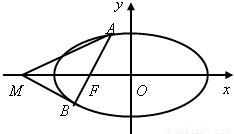
【答案】分析:(1)利用椭圆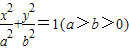 离心率为
离心率为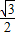 ,其上的点到左焦点F的最长距离为
,其上的点到左焦点F的最长距离为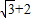 ,可建立方程组,即可求得椭圆的方程;
,可建立方程组,即可求得椭圆的方程;
(2)设M(m,0)为椭圆的左特征点,根据椭圆左焦点,设直线AB方程代入椭圆方程,由∠AMB被x轴平分,kAM+kBM=0,利用韦达定理,即可求得结论.
解答:解:(1)由题意知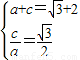 ,∴a=2,c=
,∴a=2,c=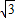 ,∴
,∴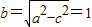
∴椭圆的方程为 ;
;
(2)设M(m,0)为椭圆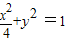 的左特征点,椭圆的左焦点F(-
的左特征点,椭圆的左焦点F(-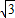 ,0),
,0),
可设直线AB的方程为x=ky-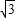 (k≠0)
(k≠0)
代入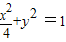 ,得:(ky-
,得:(ky-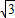 )y2+4y2=4,即(k2+4)y2-
)y2+4y2=4,即(k2+4)y2-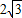 ky-1=0,
ky-1=0,
设A(x1,y1),B(x2,y2)得y1+y2=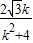 ,y1y2=-
,y1y2=-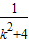
∵∠AMB被x轴平分,kAM+kBM=0,即 ,
,
即y1(ky2-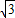 )+y2(ky1-
)+y2(ky1-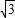 )-(y1+y2)m=0
)-(y1+y2)m=0
所以,2ky1y2-(y1+y2)(m+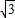 )=0
)=0
于是,2k×(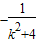 )-
)-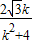 ×(m+
×(m+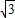 )=0
)=0
∵k≠0,∴1+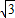 (m+
(m+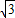 )=0,即m=
)=0,即m=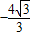 ,∴M(
,∴M(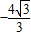 ,0)
,0)
点评:本题以新定义为载体主要考查了椭圆性质的应用,直线与椭圆相交关系的处理,要注意解题中直线AB得方程设为x=ky-2(k≠0)的好处在于避免讨论直线的斜率是否存在.
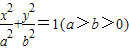 离心率为
离心率为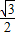 ,其上的点到左焦点F的最长距离为
,其上的点到左焦点F的最长距离为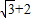 ,可建立方程组,即可求得椭圆的方程;
,可建立方程组,即可求得椭圆的方程;(2)设M(m,0)为椭圆的左特征点,根据椭圆左焦点,设直线AB方程代入椭圆方程,由∠AMB被x轴平分,kAM+kBM=0,利用韦达定理,即可求得结论.
解答:解:(1)由题意知
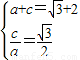 ,∴a=2,c=
,∴a=2,c=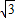 ,∴
,∴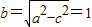
∴椭圆的方程为
 ;
;(2)设M(m,0)为椭圆
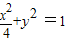 的左特征点,椭圆的左焦点F(-
的左特征点,椭圆的左焦点F(-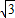 ,0),
,0),可设直线AB的方程为x=ky-
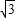 (k≠0)
(k≠0)代入
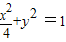 ,得:(ky-
,得:(ky-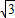 )y2+4y2=4,即(k2+4)y2-
)y2+4y2=4,即(k2+4)y2-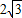 ky-1=0,
ky-1=0,设A(x1,y1),B(x2,y2)得y1+y2=
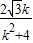 ,y1y2=-
,y1y2=-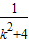
∵∠AMB被x轴平分,kAM+kBM=0,即
 ,
,即y1(ky2-
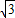 )+y2(ky1-
)+y2(ky1-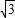 )-(y1+y2)m=0
)-(y1+y2)m=0所以,2ky1y2-(y1+y2)(m+
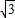 )=0
)=0于是,2k×(
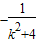 )-
)-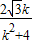 ×(m+
×(m+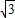 )=0
)=0∵k≠0,∴1+
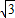 (m+
(m+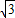 )=0,即m=
)=0,即m=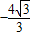 ,∴M(
,∴M(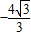 ,0)
,0)点评:本题以新定义为载体主要考查了椭圆性质的应用,直线与椭圆相交关系的处理,要注意解题中直线AB得方程设为x=ky-2(k≠0)的好处在于避免讨论直线的斜率是否存在.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
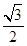 的椭圆
的椭圆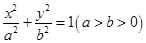 上的点到左焦点
上的点到左焦点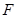 的最长距离为
的最长距离为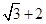 .
.
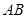 ,若点
,若点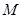 在
在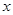 轴上,且使得
轴上,且使得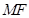 为
为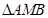 的一条内角平分线,则称点
的一条内角平分线,则称点 的椭圆
的椭圆 上的点到
上的点到 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点
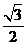 的椭圆
的椭圆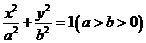 上的点到左焦点
上的点到左焦点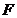 的最长距离为
的最长距离为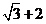 .
.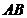 ,若点
,若点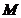 在
在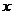 轴上,且使得
轴上,且使得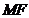 为
为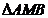 的一条内角平分线,则称点
的一条内角平分线,则称点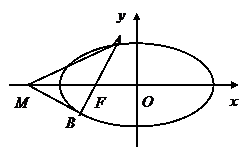
 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点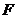 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点