题目内容
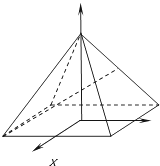
如图,已知正四棱锥S﹣ABCD的底面边长为2,高为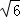 ,P为棱SC的中点.
,P为棱SC的中点.
(1)求直线AP与平面SBC所成角的正弦值;
(2)求两面角B﹣SC﹣D大小的余弦值;
(3)在正方形ABCD内是否有一点Q,使得PQ⊥平面SDC?若存在,求PQ的长;若不存在,请说明理由.
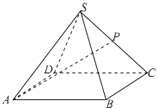
解:(1)设正方形ABCD的中心为O,如图建立空间直角坐标系,
则A(1,﹣1,0),B(1,1,0),C(﹣1,1,0),
D(﹣1,﹣1,0),S(0,0,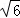 ),
),
∵P是SC的中点,∴P(﹣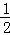 ,
,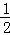 ,
,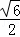 ).…(2分)
).…(2分)
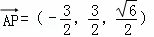 ,设平面SBC的法向量
,设平面SBC的法向量 =(x1,y1,z1),
=(x1,y1,z1),
则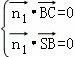 ,即
,即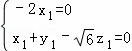 ,取
,取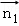 =(0,
=(0,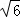 ,1),
,1),
∴cos<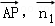 >=
>=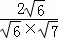 =
=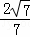 ,…(4分)
,…(4分)
故直线AP与平面SBC所成角的正弦值为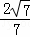 .…(6分)
.…(6分)
(2)设平面SDC的法向量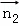 =(x2,y2,z2),则
=(x2,y2,z2),则
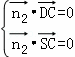 ,即
,即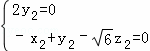 ,取
,取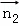 =(﹣
=(﹣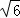 ,0,1),
,0,1),
∴cos<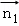 ,
,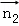 >=
>=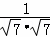 =
=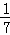 ,…(9分)
,…(9分)
又二面角B﹣SC﹣D为钝角二面角,
故二面角B﹣SC﹣D大小的余弦值为﹣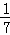 .…(11分)
.…(11分)
(3)设Q(x,y,0),则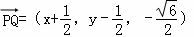 ,…(12分)
,…(12分)
若PQ⊥平面SDC,则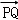 ∥
∥ ,
,
∴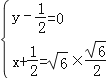 ,解得
,解得 ,…(15分)
,…(15分)
但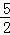 >1,点Q不在正方形ABCD内,故不存在满足条件的点Q.…(16分)
>1,点Q不在正方形ABCD内,故不存在满足条件的点Q.…(16分)

练习册系列答案
相关题目
 ,OM=1,则MN= _________ .
,OM=1,则MN= _________ .
 服从正态分布
服从正态分布 ,若
,若 ,则
,则

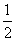 B.1 C.-
B.1 C.- 中,已知
中,已知 ,则
,则 .
. 是( )
是( )