题目内容
(2012•南宁模拟)已知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE、SD所成的角的余弦值为
.
| ||
| 3 |
| ||
| 3 |
分析:根据异面直线所成角的定义可得分别取SC,DC,AD边的中点F,G,H易得EF
HA故四边形AEFH为平行四边形所以AE∥DF,又根据中点的性质可得FG∥SD从而将异面直线转化为了相交直线即∠HFG或其补角即为异面直线AE、SD所成的角然后再利用余弦定理求∠HFG得余弦值即可.
| ||
. |
解答: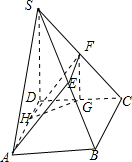
解:由于正四棱锥S-ABCD的侧棱长与底面边长都相等故不妨设棱长为a
取SC的中点F连接EF则EF∥
BC,取AD的中点H连接HF则可得EF
HA故四边形AEFH为平行四边形所以AE∥HF
再取DC中点G连接HG则FG∥SD所以∠HFG或其补角即为异面直线AE、SD所成的角
∵HF=AE=
a,FG=
a,HG=
=
a
∴cos∠HFG=
=
>0
即AE、SD所成的角的余弦值为

解:由于正四棱锥S-ABCD的侧棱长与底面边长都相等故不妨设棱长为a
取SC的中点F连接EF则EF∥
| 1 |
| 2 |
| ||
. |
再取DC中点G连接HG则FG∥SD所以∠HFG或其补角即为异面直线AE、SD所成的角
∵HF=AE=
| ||
| 2 |
| 1 |
| 2 |
| DH2+DG2 |
| ||
| 2 |
∴cos∠HFG=
| HF2+FG2- HG2 |
| 2HF×FG |
| ||
| 3 |
即AE、SD所成的角的余弦值为
| ||
| 3 |
点评:本题主要考查了异面直线所成的角.解题的关键是要紧紧抓住利用平行的传递性(通常利用平行四边形的性质或中位线定理)将异面直线转化为相交直线然后在三角形中利用余弦定理求解(要注意的是利用于余弦值的正负判断是这个角还是这个角的补角)!

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (2012•南宁模拟)如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为
(2012•南宁模拟)如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为