题目内容
已知数列{an}的前n项和为Sn=-![]() n2+
n2+![]() n,求数列{|an|}的前n项和Tn.
n,求数列{|an|}的前n项和Tn.
(1)当n≤34时,
Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-![]() n2+
n2+![]() n.
n.
(2)当n≥35时,
Tn=|a1|+|a2|+…+|a34|+|a35|+|a36|+…+|an|.
=(a1+a2+…+a34)-(a35+a36+…+an)
=2(a+a2+…+a34)-(a1+a2+…an)
=2S34-Sn
=2(-![]() ×342+
×342+![]() ×34)-(-
×34)-(-![]() n2+
n2+![]() n)
n)
=![]() n2-
n2-![]() n+3 502,
n+3 502,
故Tn=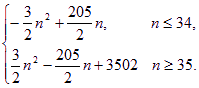
解析:
a1=S1=-![]() +
+![]() =101.
=101.
当n≥2时,an=Sn-Sn-1=-3n+104.
∵a1也适合an=-3n+104,
∴数列{an}的通项公式为an=-3n+104(n∈N*).
由an=-3n+104≥0,得n≤34.7,
即当n≤34时,an>0;当n≥35时,an<0.
(1)当n≤34时,
Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=-![]() n2+
n2+![]() n.
n.
(2)当n≥35时,
Tn=|a1|+|a2|+…+|a34|+|a35|+|a36|+…+|an|.
=(a1+a2+…+a34)-(a35+a36+…+an)
=2(a+a2+…+a34)-(a1+a2+…an)
=2S34-Sn
=2(-![]() ×342+
×342+![]() ×34)-(-
×34)-(-![]() n2+
n2+![]() n)
n)
=![]() n2-
n2-![]() n+3 502,
n+3 502,
故Tn=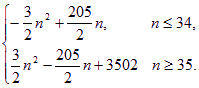

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |