题目内容
定义函数f(x)=[x[x]],其中[x]表示不超过x的最大整数,如:[1.5]=1,[-1.3]=-2,当x∈[0,n)(n∈N*)时,设函数f(x)的值域为A,记集合A中的元素个数为an,则式子[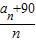 ]的最小值为 .
]的最小值为 .
【答案】分析:先由题意先求[x],再求x[x],然后再求[x[x]],得到an,进而得到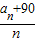 ,用基本不等式求解.
,用基本不等式求解.
解答:解:根据题意:[x]=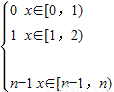
∴x[x]=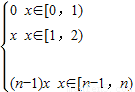
∴[x[x]]在各区间中的元素个数是:1,1,2,3,…,n
∴an=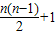
∴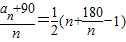 ,所以当n=13或14时,最小值为13.
,所以当n=13或14时,最小值为13.
故答案为:13
点评:本题主要通过取整函数来建立新函数,进而研究其定义域和值域.
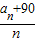 ,用基本不等式求解.
,用基本不等式求解.解答:解:根据题意:[x]=
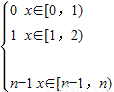
∴x[x]=
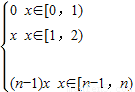
∴[x[x]]在各区间中的元素个数是:1,1,2,3,…,n
∴an=
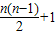
∴
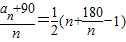 ,所以当n=13或14时,最小值为13.
,所以当n=13或14时,最小值为13.故答案为:13
点评:本题主要通过取整函数来建立新函数,进而研究其定义域和值域.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目