题目内容
【题目】如图,墙上有一壁画,最高点![]() 离地面4米,最低点
离地面4米,最低点![]() 离地面2米,观察者从距离墙
离地面2米,观察者从距离墙![]() 米,离地面高
米,离地面高![]() 米的
米的![]() 处观赏该壁画,设观赏视角
处观赏该壁画,设观赏视角![]()
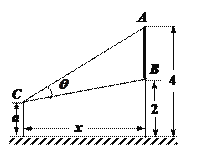
(1)若![]() 问:观察者离墙多远时,视角
问:观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() 当
当![]() 变化时,求
变化时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]()
(2)3≤x≤4.
【解析】
试题(1)利用两角差的正切公式建立函数关系式,根据基本不等式求![]() 最值,最后根据正切函数单调性确定
最值,最后根据正切函数单调性确定![]() 最大时取法,(2)利用两角差的正切公式建立等量关系式,进行参变分离得
最大时取法,(2)利用两角差的正切公式建立等量关系式,进行参变分离得![]() ,再根据a的范围确定
,再根据a的范围确定![]() 范围,最后解不等式得
范围,最后解不等式得![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,过
时,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
则![]() ,且
,且![]() ,
,
由已知观察者离墙![]() 米,且
米,且![]() ,
,
则![]() ,
,
所以,![]()
 ,
,
当且仅当![]() 时,取“
时,取“![]() ”.
”.
又因为![]() 在
在![]() 上单调增,所以,当观察者离墙
上单调增,所以,当观察者离墙![]() 米时,视角
米时,视角![]() 最大.
最大.
(2)由题意得,![]() ,又
,又![]() ,
,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.


练习册系列答案
相关题目
【题目】读书可以使人保持思想活力,让人得到智慧启发,让人滋养浩然正气书籍是文化的重要载体,读书是承继文化的重要方式某地区为了解学生课余时间的读书情况,随机抽取了![]() 名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于
名学生进行调查,根据调查得到的学生日均课余读书时间绘制成如图所示的频率分布直方图,将日均课余读书时间不低于![]() 分钟的学生称为“读书之星”,日均课余读书时间低于
分钟的学生称为“读书之星”,日均课余读书时间低于![]() 分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于
分钟的学生称为“非读书之星”:已知抽取的样本中日均课余读书时间低于![]() 分钟的有
分钟的有![]() 人
人
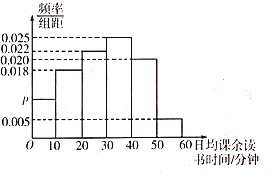
(1)求![]() 的值;
的值;
(2)根据已知条件完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“读书之星”与性别有关?
以上的把握认为“读书之星”与性别有关?
非读书之星 | 读书之星 | 总计 | |
男 | |||
女 |
|
| |
总计 |
(3)将上述调查所得到的频率视为概率,现从该地区大量学生中,随机抽取![]() 名学生,每次抽取
名学生,每次抽取![]() 名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量
名,已知每个人是否被抽到互不影响,记被抽取的“读书之星”人数为随机变量![]() ,求
,求![]() 的分布列和期望
的分布列和期望![]()
附: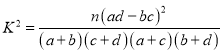 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|