题目内容
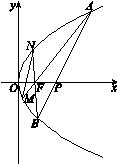
(本题12分)已知椭圆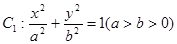 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线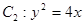 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且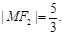
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线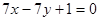 上,求直线AC的方程。
上,求直线AC的方程。
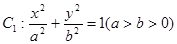 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线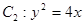 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且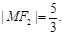
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线
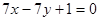 上,求直线AC的方程。
上,求直线AC的方程。(I) (II)直线AC的方程为
(II)直线AC的方程为
 (II)直线AC的方程为
(II)直线AC的方程为
试题分析:(I)设
 由抛物线定义,
由抛物线定义,
 ,
,  M点C1上,
M点C1上,

 舍去.
舍去.
 椭圆C1的方程为
椭圆C1的方程为
(II)
 为菱形,
为菱形, ,设直线AC的方程为
,设直线AC的方程为

 在椭圆C1上,
在椭圆C1上, 设
设 ,则
,则

 的中点坐标为
的中点坐标为 ,由ABCD为菱形可知,点
,由ABCD为菱形可知,点 在直线BD:
在直线BD: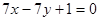 上,
上,
 ∴直线AC的方程为
∴直线AC的方程为
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了抛物线的定义及椭圆的几何性质。为求直线AC的方程,本题利利用了待定系数法,通过联立方程组,应用韦达定理,确定了AC、BD的中点坐标,代人已知方程,得到“待定系数”,达到了解题目的。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
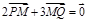 ,
,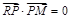 .
.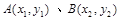 为轨迹C上两点,且
为轨迹C上两点,且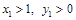 ,N(1,0),求实数
,N(1,0),求实数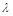 ,使
,使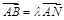 ,且
,且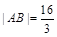 .
.



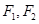 为双曲线C:
为双曲线C: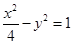 的左、右焦点,点
的左、右焦点,点 在
在 上,
上,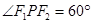 ,则P到
,则P到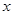 轴的距离为 ( )
轴的距离为 ( )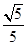
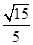
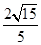
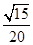
 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则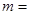 ( )
( )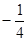
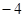
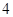
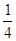
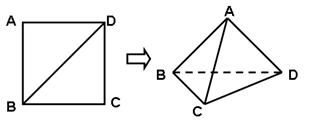
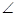 ABD为二面角A-BC-D的平面角;(2)AC
ABD为二面角A-BC-D的平面角;(2)AC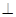 BD;(3) △ACD是等边三角形;
BD;(3) △ACD是等边三角形;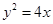 的焦点为
的焦点为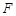 .过点
.过点 的直线交抛物线于
的直线交抛物线于 ,
, 两点,直线
两点,直线 ,
,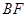 分别与抛物线交于点
分别与抛物线交于点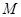 ,
,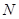 .
.
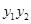 的值;
的值;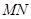 的斜率为
的斜率为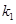 ,直线
,直线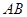 的斜率为
的斜率为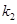 .证明:
.证明: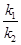 为定值.
为定值. 的准线方程是
的准线方程是 的值为 。
的值为 。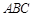 的两个顶点
的两个顶点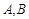 的坐标分别是
的坐标分别是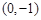 ,
,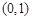 ,且
,且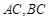 所在直线的斜率之积等于
所在直线的斜率之积等于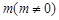 .
.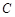 的轨迹
的轨迹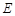 的方程,并判断轨迹
的方程,并判断轨迹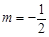 时,过点
时,过点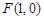 的直线
的直线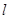 交曲线
交曲线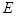 于
于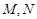 两点,设点
两点,设点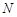 关于
关于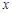 轴的对称点为
轴的对称点为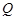 (
(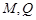 不重合).求证直线
不重合).求证直线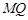 与
与