题目内容
已知向量
=(x,8),
(4,y),
(x,y)(x>0,y>0),若
∥
,则|
|的最小值为( )
| a |
| b |
| c |
| a |
| b |
| c |
A、4
| ||
| B、4 | ||
| C、64 | ||
| D、8 |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的运算
专题:平面向量及应用
分析:由向量共线的条件得到xy=32,求出|
|后利用基本不等式得最小值.
| c |
解答:解:∵向量
=(x,8),
(4,y),且
∥
,
∴xy-32=0,即xy=32.
又
=(x,y),且x>0,y>0,
∴|
|=
≥
=
=8.
∴|
|的最小值为8.
故选:D.
| a |
| b |
| a |
| b |
∴xy-32=0,即xy=32.
又
| c |
∴|
| c |
| x2+y2 |
| 2xy |
| 2×32 |
∴|
| c |
故选:D.
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0.是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 已知某算法的流程图如图所示,若输入的有序数对(x,y)为(7,6),则输出的有序数对(x,y)为( )
已知某算法的流程图如图所示,若输入的有序数对(x,y)为(7,6),则输出的有序数对(x,y)为( )| A、(14,13) | B、(13,14) | C、(11,12) | D、(12,11) |
 将1﹑2﹑3﹑4四个数字随机填入右方2×2的方格中﹐每个方格中恰填一数字﹐但数字可重复使用﹒试问事件「A方格的数字大于B方格的数字﹑且C方格的数字大于D方格的数字」的机率为( )
将1﹑2﹑3﹑4四个数字随机填入右方2×2的方格中﹐每个方格中恰填一数字﹐但数字可重复使用﹒试问事件「A方格的数字大于B方格的数字﹑且C方格的数字大于D方格的数字」的机率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
在区间[-π,π]上的图象是( )
| xcosx |
| x2+1 |
A、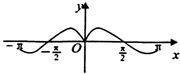 |
B、 |
C、 |
D、 |
如图,在四面体OABC中,AC=BC,|
|=3,|
|=1,则
•
=( )

| OA |
| OB |
| OC |
| BA |

| A、8 | B、6 | C、4 | D、3 |
矩形ABCD中,AB=2,AD=1,点E、F分别为BC、CD边上动点,且满足EF=1,则
•
的最小值为( )
| AE |
| AF |
| A、3 | ||
| B、4 | ||
C、5+
| ||
D、5-
|
若等差数列{an}的前n项和为Sn,且S3=12,a1=2,则a4=( )
| A、20 | B、10 | C、6 | D、8 |
 如图,点P从点O出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系分别记为y=f(x),y=g(x),定义函数h(x)=
如图,点P从点O出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系分别记为y=f(x),y=g(x),定义函数h(x)=