题目内容
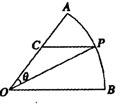
如图所示,扇形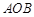 ,圆心角
,圆心角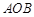 的大小等于
的大小等于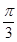 ,半径为2,在半径
,半径为2,在半径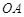 上有一动点
上有一动点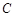 ,过点
,过点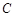 作平行于
作平行于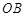 的直线交弧
的直线交弧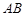 于点
于点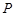 .
.
(1)若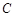 是半径
是半径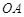 的中点,求线段
的中点,求线段 的长;
的长;
(2)设 ,求
,求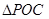 面积的最大值及此时
面积的最大值及此时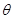 的值.
的值.
(1)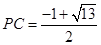 ;(2)当
;(2)当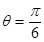 时,
时,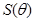 取得最大值
取得最大值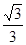 .
.
解析试题分析:(1)由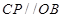 得出
得出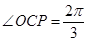 ,在
,在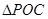 中,利用余弦定理计算
中,利用余弦定理计算 长度;(2)要求
长度;(2)要求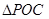 面积的最大值,需要将面积表示为
面积的最大值,需要将面积表示为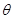 的函数再求最值,显然可以用正弦的面积公式,注意到
的函数再求最值,显然可以用正弦的面积公式,注意到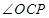 已知,故不妨用
已知,故不妨用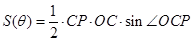 ,接下来分别把
,接下来分别把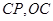 表示成
表示成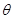 的函数,在
的函数,在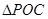 中利用正弦定理
中利用正弦定理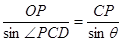 得
得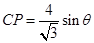 ,同理,利用正弦定理
,同理,利用正弦定理 ,得
,得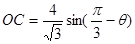 ,故
,故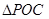 的面积
的面积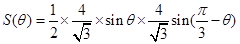 ,运用两角差的正弦公式,降幂公式以及辅助角公式将
,运用两角差的正弦公式,降幂公式以及辅助角公式将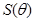 化为同角三角函数,得
化为同角三角函数,得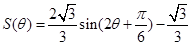 ,注意
,注意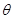 的范围是
的范围是 ,可得
,可得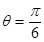 时
时 取最大值1,此时
取最大值1,此时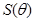 取最大值
取最大值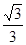 .
.
试题解析:(1)在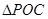 中,
中,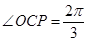 ,
, ,由
,由
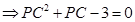
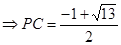 ; 5分
; 5分
(2) 平行于
平行于
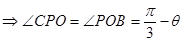 ,
,
在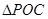 中,由正弦定理得
中,由正弦定理得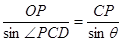 ,即
,即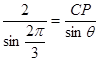 ,
, 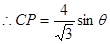 ,
,
又 ,
,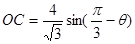 . 8分
. 8分
记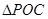 的面积为
的面积为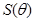 ,则
,则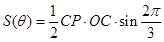
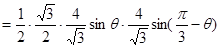

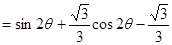
=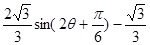 , 10分
, 10分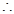 当
当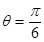 时,
时,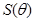 取得最大值
取得最大值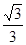 . 12分
. 12分
考点:1、三角恒等变换;2、三角函数的基本运算;3、正、余弦定理.

练习册系列答案
相关题目
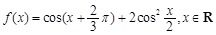 .
. 的值域;
的值域;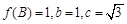 ,求a的值.
,求a的值.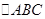 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,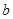 ,
,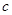 ,且满足
,且满足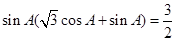
 ,
,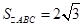 ,求
,求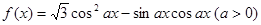 的图像与直线
的图像与直线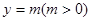 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为 的等差数列.
的等差数列.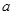 和
和 的值;
的值; 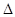 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若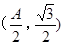 是函数
是函数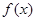 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求 中,角
中,角 的对边分别为
的对边分别为 且
且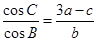 .
.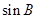 ;
; ,求
,求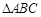 中,内角
中,内角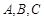 的对边分别为
的对边分别为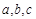 ,且
,且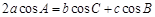 .
.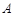 的大小;
的大小;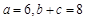 ,求
,求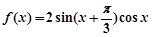 .
.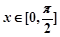 ,求
,求 的取值范围;
的取值范围;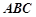 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知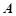 为锐角,
为锐角,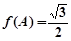 ,
,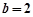 ,
,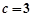 ,求
,求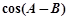 的值.
的值.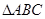 中,
中,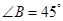 ,
, ,
,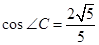 ,点
,点 是
是 的中点, 求:
的中点, 求: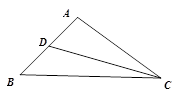
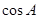 的值和中线
的值和中线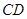 的长
的长