题目内容
若数列{an}满足an=qn(q>0,n∈N*)则以下命题中正确的是 .①{a2n}是等比数列
②
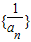 是等比数列
是等比数列③lgan是等差数列
④{lgan2}是等差数列.
【答案】分析:利用等差数列和等比数列的定义分别进行判断即可.
解答:解:因为q>0,所以数列an=qn(q>0,n∈N*)为等比数列,公比为q.
①则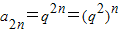 ,为等比为q2 的等比数列,所以①正确.
,为等比为q2 的等比数列,所以①正确.
②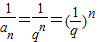 ,所以为等比数列,公比为
,所以为等比数列,公比为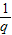 .所以②正确.
.所以②正确.
③因为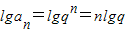 ,所以lgan是等差数列,公差为lgq,所以③正确.
,所以lgan是等差数列,公差为lgq,所以③正确.
④因为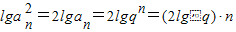 ,所以{lgan2}是等差数列.公差为2lgq,所以④正确.
,所以{lgan2}是等差数列.公差为2lgq,所以④正确.
故答案为:①②③④.
点评:本题主要考查等差数列和等比数列的判断,比较基础.
解答:解:因为q>0,所以数列an=qn(q>0,n∈N*)为等比数列,公比为q.
①则
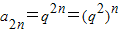 ,为等比为q2 的等比数列,所以①正确.
,为等比为q2 的等比数列,所以①正确.②
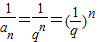 ,所以为等比数列,公比为
,所以为等比数列,公比为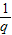 .所以②正确.
.所以②正确.③因为
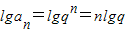 ,所以lgan是等差数列,公差为lgq,所以③正确.
,所以lgan是等差数列,公差为lgq,所以③正确.④因为
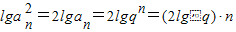 ,所以{lgan2}是等差数列.公差为2lgq,所以④正确.
,所以{lgan2}是等差数列.公差为2lgq,所以④正确.故答案为:①②③④.
点评:本题主要考查等差数列和等比数列的判断,比较基础.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )

 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
