Question

【题目】如图，在四棱柱 中，侧面和侧面都是矩形， 是边长为的正三角形， 分别为的中点.

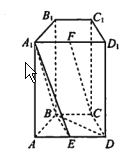
（1）求证： 平面；

（2）求证：平面平面.

（3）若平面，求棱的长度.

Answer 1

【答案】(1)详见解析; (2)详见解析; （3）1.

【解析】试题分析：（1）本问考查线面垂直的证明，根据线面垂直判定定理可知，应证明与平面ABCD内的两条相交直线垂直，根据已知条件侧面和侧面都是矩形，所以，且，于是问题得证；（2）本问考查面面垂直的证明，应先证明线面垂直，根据题中条件为正三角形，E为AD中点，所以BEAD，根据面面垂直的性质定理，则BE平面， 平面，所以问题得证；（3）本问考查线面平行的性质定理，确定经过CF的平面与平面的交线，从而得到CF平行于交线，然后根据平面几何知识求BC的长度.

试题解析：(1)因为侧面和侧面都是矩形，所以，且.因为，所以平面.

(2)因为是正三角形，且为中点,所以，因为平面，而平面，所以.因为，所以平面，因为平面，所以平面平面.

（3）因为，而为的中点，所以，所以四点共面.因为平面，而平面平面，所以.所以四边形是平行四边形.所以.