题目内容
已知F![]() 、F
、F![]() 为双曲线
为双曲线![]() (a>0,b>0)的焦点,过F
(a>0,b>0)的焦点,过F![]() 作垂直于x轴的直线交双曲线于点P,且∠PF
作垂直于x轴的直线交双曲线于点P,且∠PF![]() F
F![]() =30
=30![]() ,求双曲线的渐近线方程。
,求双曲线的渐近线方程。
双曲线的渐近线方程为y=±![]() x
x
解析:
设F![]() (c,0)(c>0),P(c,y
(c,0)(c>0),P(c,y![]() ),则
),则![]() ,解得y
,解得y![]() =±
=±![]() 。
。
∴|P F![]() |=
|=![]() 。
。
又∵在直角三角形P F![]() F
F![]() 中,∠PF
中,∠PF![]() F
F![]() =30
=30![]()
解法一:|F![]() F
F![]() |=
|=![]() |P F
|P F![]() |,即2c=
|,即2c=![]()
![]() 将c
将c![]() =a
=a![]() +b
+b![]() 代入,解得b
代入,解得b![]() =2 a
=2 a![]()
解法二:|PF![]() |=2|P F
|=2|P F![]() |,由双曲线定义可知,|PF
|,由双曲线定义可知,|PF![]() |-|P F
|-|P F![]() |=2a,得|P F
|=2a,得|P F![]() |=2a
|=2a
∵|P F![]() |=
|=![]() ,∴2a=
,∴2a=![]() ,即b
,即b![]() =2 a
=2 a![]() ∴
∴![]() =
=![]()
故所求双曲线的渐近线方程为y=±![]() x 。
x 。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
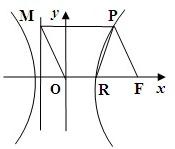 如图,F为双曲线C:
如图,F为双曲线C: