题目内容
函数![]() 的定义域为(0,1](
的定义域为(0,1](![]() 为实数).
为实数).
⑴当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
⑵若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
⑶求函数![]() 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时![]() 的值
的值
(1)![]() (2)
(2)![]()
(3)
当![]() 时,无最小值,当
时,无最小值,当![]() 时取得最大值
时取得最大值![]() ;
;
![]() 时,无最大值,当x=1时取得最小值2-a;
时,无最大值,当x=1时取得最小值2-a;
当![]() 时,无最大值,当
时,无最大值,当![]() 时取得最小值
时取得最小值![]()
解析:
(1)显然函数![]() 的值域为
的值域为![]() ;
;
(2)若函数![]() 在定义域上是减函数,则任取
在定义域上是减函数,则任取![]()
![]() 且
且![]() 都有
都有
![]() 成立, 即
成立, 即![]()
只要![]() 即可,
即可,
由![]()
![]() ,故
,故![]() ,所以
,所以![]() ,
,
故![]() 的取值范围是
的取值范围是![]() ;
;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调增,无最小值,
上单调增,无最小值,
当![]() 时取得最大值
时取得最大值![]() ;
;
由(2)得当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,无最大值,
上单调减,无最大值,
当x=1时取得最小值2-a;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增,无最大值,
上单调增,无最大值,
当![]() 时取得最小值
时取得最小值![]()

练习册系列答案
相关题目
 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为 ,则m的取值范围是( )
,则m的取值范围是( ) C.
C. 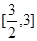 D.
D.  )
) 的定义域为[0,1]且同时满足:①对任意
的定义域为[0,1]且同时满足:①对任意 ②
②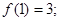 ③若
③若
 的值;
的值; 的前n项和为Sn,且
的前n项和为Sn,且 ,
,
 的定义域为[0 ,m],值域为
的定义域为[0 ,m],值域为 ,则 m的取值范围是______________
,则 m的取值范围是______________