题目内容
与四面体的一个面及另外三个面的延长面都相切的球称为该四面体的旁切球,则棱长为1的正四面体的旁切球的半径r=
.
| ||
| 6 |
| ||
| 6 |
分析:先根据题意作出图形,如图所示,圆O是棱长为1的正四面体ABCD的旁切球的大圆,AF是正四面体ABCD的高,F是底面三角形BCD的中心,AG是大圆O的切线,G为切点,设大圆的半径为R,在三角形ABC中,求出AE,在直角三角形AEF中,求出AF,再利用△AOG∽△AEF,得出关于R的方程即可求出答案.
解答: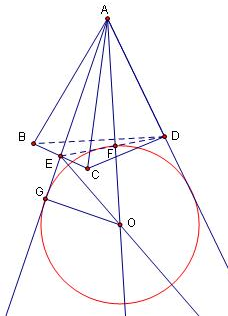 解:根据题意作出图形,如图所示,圆O是棱长为1的正四面体ABCD的旁切球的大圆,AF是正四面体A-BCD的高,F是底面三角形BCD的中心,AE是侧面上的中线,AG是大圆O的切线,G为切点,设大圆的半径为R,
解:根据题意作出图形,如图所示,圆O是棱长为1的正四面体ABCD的旁切球的大圆,AF是正四面体A-BCD的高,F是底面三角形BCD的中心,AE是侧面上的中线,AG是大圆O的切线,G为切点,设大圆的半径为R,
在三角形ABC中,AE=
=ED,
在直角三角形AEF中,EF=
ED=
×
=
,
∴AF=
=
,
在三角形AOG和三角形AEF中,∵∠OAG=∠EAF,∠AGO=∠AFE=90°,
∴△AOG∽△AEF,
∴
=
即
=
,
∴R=
.
故答案为:
.
 解:根据题意作出图形,如图所示,圆O是棱长为1的正四面体ABCD的旁切球的大圆,AF是正四面体A-BCD的高,F是底面三角形BCD的中心,AE是侧面上的中线,AG是大圆O的切线,G为切点,设大圆的半径为R,
解:根据题意作出图形,如图所示,圆O是棱长为1的正四面体ABCD的旁切球的大圆,AF是正四面体A-BCD的高,F是底面三角形BCD的中心,AE是侧面上的中线,AG是大圆O的切线,G为切点,设大圆的半径为R,在三角形ABC中,AE=
| ||
| 2 |
在直角三角形AEF中,EF=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
∴AF=
| AE2-EF2 |
| ||
| 3 |
在三角形AOG和三角形AEF中,∵∠OAG=∠EAF,∠AGO=∠AFE=90°,
∴△AOG∽△AEF,
∴
| AO |
| OG |
| AE |
| EF |
| ||||
| R |
| ||||
|
∴R=
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本小题主要考查球内接多面体、棱锥的几何特征、三角形相似等基础知识,考查运算求解能力,考查空间想象能力.属于基础题.

练习册系列答案
相关题目
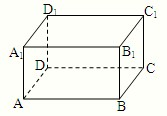 如图,以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体.
如图,以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体.