题目内容
某海域设立东西方向两个观测点A、B，相距
海里．现接到一艘渔船发出的求救讯号，测出该船位于点A北偏东30°，点B北偏西60°的C点．立刻通知位于B观测点南偏西60°且与B点相距16海里的D处的救援船前去营救，若救援船以28海里/小时的航速前往，问需要多长时间到达C处？
解：如图：由题意知△ABC为直角三角形，∠ACB＝90°，
AB＝
，
∴BC＝ABcos30°＝10，
又∵BD＝16，∠CBD＝60°，
在△BCD中，根据余弦定理得：
DC2＝BC2＋BD2－2BC·BD cos60°＝102＋162－2×10×1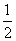6×
＝196，
∴DC＝14（海里），则需要的时间为 t＝
＝0.5小时．
练习册系列答案
名校课堂系列答案
相关题目
的圆心坐标是 ．
，则x+y的最小值是 _________ ．
在等差数列{an}中，若a2=2，a12=12，那么a4+a19=（ ）
|
| A． | 10 | B． | 23 | C． | 28 | D． | 60 |
m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题正确的是（ ）
|
| A． | 若α⊥β，α⊥γ，则β⊥γ | B． | 若m、n与α所成的角相等，则m∥n |
|
| C． | 若m⊥α，m∥β，则α⊥β | D． | 若m∥n，m⊂α，则n∥α |
用反证法证明命题“：若 a，b∈N，ab能被3整除，那么a，b中至少有一个能被3整除”时，假设应为（ ）
|
| A． | a，b都能被3整除 | B． | a不能被3整除 |
|
| C． | a，b不都能被3整除 | D． | a，b都不能被3整除 |
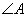与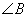
是两条平行直线的同位角，则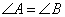
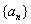中，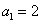
，
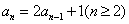，由此归纳出