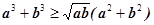题目内容
已知n个圆中每两个圆相交于两点,且无三圆过同一点,用数学归纳法证明:这n个圆将平面划分成n2-n+2块区域.
思路分析:用数学归纳法解几何问题.
证明:(Ⅰ)当n=1时,1个圆将平面分成2部分,而2=12-1+2,
∴当n=1时命题正确.
(Ⅱ)假设n=k时命题正确,即满足条件的k个圆将平面划分成k2-k+2部分,
∴当n=k+1时,平面上增加了第k+1个圆,它与原来的k个圆的每一个圆都相交于两个不同点,共2k个交点.而这2k个点将第k+1个圆分成2k段弧,每段弧将原来的一块区域隔成了两块区域,∴区域的块数增加了2k块,
∴k+1个圆将平面划分成的块数为
(k2-k+2)+2k=k2+k+2=(k+1)2-(k+1)+2,
∴n=k+1时命题也正确,
根据(Ⅰ)(Ⅱ)知命题对n∈N*都正确.
误区警示
用数学归纳法证明几何问题是教材中一种题型,但由于这种题型的证明主要是文字推理为主,所以语言一定精确,要能准确地描述第二步的假设,合理清晰地推导出结论.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
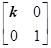 ,N=
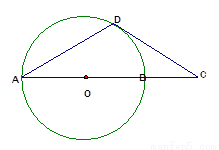
,N=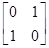 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值

 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
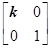 ,N=
,N=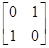 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值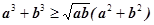
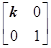 ,N=
,N=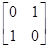 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值