Question

抛物线y²=4x与直线x+y-2=0的交点为A，B，抛物线的顶点为O，在抛物线弧AOB上求一点C，使△ABC的面积最大，并求出这个最大面积.

Answer 1

解析：利用直线与曲线关系、最值问题、点到直线的距离公式求解.

解法一：如图，设与直线AB平行且与抛物线相切的直线方程为x+y-b=0.?

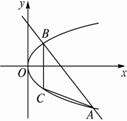
将它与抛物线方程y²=4x联立，得y²=4（b-y）.?

即y²+4y-4b=0.?

由Δ=4²-4（-4b）=0，b=-1，若切线为x+y+1=0，求得切点为C（1，-2）.因直线x+y+1=0与x+y-2=0的距离为d==.由，?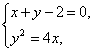

解得交点坐标为A（4+2，-2-2），?

B（，），?

∴|AB|=，于是?

S_△ABC=|AB|·d=.?

即当C点为（1，-2）时，S_△ABC的最大值为6.

解法二：设C点的坐标为（，y₀），则C点与AB距离为d===

.?

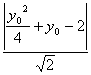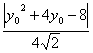∵点C的纵坐标值介于A，B两点的纵坐标值之间.?

∴-2-2≤y₀≤-2+2，故当y₀=-2时，有d_max=.?

此时C点的坐标为（1，-2），仿上得S_△ABC最大值为6.

点评：此题是关于直线与曲线关系，三角形面积取得最大值的一道综合题，但问题的关键是C点的取得及作用，此题的两种解法是关于曲线上的点到定直线距离取最大值的典型解法.