Question

【题目】对于函数f（x）= ，有下列5个结论： ①任取x1 ， x2∈[0，+∞），都有|f（x1）﹣f（x2）|≤2；
②函数y=f（x）在区间[4，5]上单调递增；
③f（x）=2kf（x+2k）（k∈N+），对一切x∈[0，+∞）恒成立；
④函数y=f（x）﹣ln（x﹣1）有3个零点；
⑤若关于x的方程f（x）=m（m＜0）有且只有两个不同实根x1 ， x2 ， 则x1+x2=3．
则其中所有正确结论的序号是 ． （请写出全部正确结论的序号）

Answer 1

【答案】①④⑤
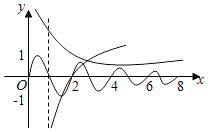
【解析】解：f（x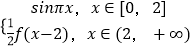）= 的图象如图所示：①∵f（x）的最大值为1，最小值为﹣1，

∴任取x1、x2∈[0，+∞），都有|f（x1）﹣f（x2）|≤2恒成立，故①正确；②函数在区间[4，5]上的单调性和[0，1]上的单调性相同，则函数y=f（x）在区间[4，5]上不单调；故②错误；③f（ ）=2f（ +2）=4f（ +4）=6f（ +6）≠8f（ +8），故不正确；故③错误，④如图所示，函数y=f（x）﹣ln（x﹣1）有3个零点；故④正确，⑤当1≤x≤2时，函数f（x）关于x= 对称，若关于x的方程f（x）=m（m＜0）有且只有两个不同实根x1，x2，

则 = ，则x1+x2=3成立，故⑤正确，

所以答案是：①④⑤．

【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案，需要熟知两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．