题目内容
在△ABC中,若sin( +A)cos(A+C-
+A)cos(A+C- π)=1,则△ABC为
π)=1,则△ABC为
- A.等腰三角形
- B.直角三角形
- C.等腰直角三角形
- D.等边三角形
C
分析:通过已知关系式,推出sin( +A)=1,且 cos(A+C-
+A)=1,且 cos(A+C- π)=1,求出A,B,C的大小,即可判断三角形的形状.
π)=1,求出A,B,C的大小,即可判断三角形的形状.
解答:∵0≤sin( +A)≤1,
+A)≤1,
0≤cos(A+C- π)≤1,
π)≤1,
由sin( +A)cos(A+C-
+A)cos(A+C- π)=1,
π)=1,
故:sin( +A)=1,且 cos(A+C-
+A)=1,且 cos(A+C- π)=1,
π)=1,
A= ,A+C-
,A+C- π=0
π=0
A= ,C=
,C= ,B=
,B= ,
,
故三角形ABC是等腰直角三角形.
故选C.
点评:本题考查三角形的形状的判定,三角函数值的范围的应用,考查灵活解题能力,计算能力.
分析:通过已知关系式,推出sin(
 +A)=1,且 cos(A+C-
+A)=1,且 cos(A+C- π)=1,求出A,B,C的大小,即可判断三角形的形状.
π)=1,求出A,B,C的大小,即可判断三角形的形状.解答:∵0≤sin(
 +A)≤1,
+A)≤1,0≤cos(A+C-
 π)≤1,
π)≤1,由sin(
 +A)cos(A+C-
+A)cos(A+C- π)=1,
π)=1,故:sin(
 +A)=1,且 cos(A+C-
+A)=1,且 cos(A+C- π)=1,
π)=1,A=
 ,A+C-
,A+C- π=0
π=0 A=
 ,C=
,C= ,B=
,B= ,
,故三角形ABC是等腰直角三角形.
故选C.
点评:本题考查三角形的形状的判定,三角函数值的范围的应用,考查灵活解题能力,计算能力.

练习册系列答案
相关题目
在△ABC中,若sin(A+B-C)=sin(A-B+C),则△ABC必是( )
| A、等腰三角形 | B、直角三角形 | C、等腰或直角三角形 | D、等腰直角三角形 |
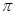 -A)=
-A)=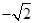 sin(
sin(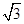 cosA=
cosA=