题目内容
实数列a0，a1，a2，a3，...由下述等式定义：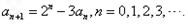
（1）若a0为常数，求a1，a2，a3的值；
（2）令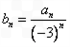
，求数列{bn}（n∈N）的通项公式（用a0、n来表示）；
（3）是否存在实数a0，使得数列{an}（n∈N）是单调递增数列？若存在，求出a0的值；若不存在，说明理由。
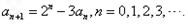
（1）若a0为常数，求a1，a2，a3的值；
（2）令
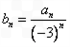，求数列{bn}（n∈N）的通项公式（用a0、n来表示）；（3）是否存在实数a0，使得数列{an}（n∈N）是单调递增数列？若存在，求出a0的值；若不存在，说明理由。
解：（1）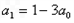
， 
， 
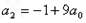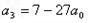
（2）由
得
即
∴
∴
∴
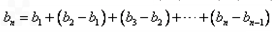
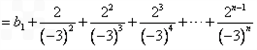
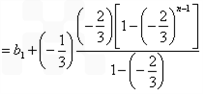
（3）
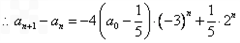
要使{an}为递增数列，则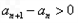
对任意n∈N*恒成立，
当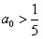
时，∵|-3|＞2，∴当
且n为偶数时，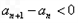
当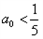
时，∵|-3|＞2，∴当
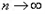且n为奇数时，
而当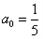
时，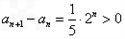
对任意n∈N*恒成立
∴存在实数
，使得数列{an}是单调递增数列
练习册系列答案
相关题目
．
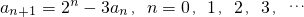