题目内容
已知椭圆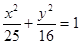 上的一点
上的一点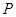 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为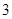 ,则
,则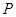 到另一焦点距离为 ( )
到另一焦点距离为 ( )
A.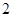 | B.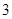 | C.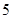 | D.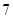 |
D
解析试题分析:由方程可知椭圆中 ,长轴为10,由椭圆定义可知
,长轴为10,由椭圆定义可知 ,所以
,所以 到另一焦点距离为
到另一焦点距离为
考点:椭圆定义
点评:定义:椭圆上的点到两焦点的距离之和为定值
 ,利用定义可由椭圆上的点到一个焦点的距离求出到另一个焦点的距离
,利用定义可由椭圆上的点到一个焦点的距离求出到另一个焦点的距离

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点 在直线
在直线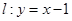 上,若存在过
上,若存在过 的直线交抛物线
的直线交抛物线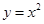 于
于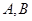 两点,且
两点,且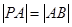 ,则称点
,则称点 为“
为“ 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )
A.直线 上的所有点都是“ 上的所有点都是“ 点” 点” | B.直线 上仅有有限个点是“ 上仅有有限个点是“ 点” 点” |
C.直线 上的所有点都不是“ 上的所有点都不是“ 点” 点” | D.直线 上有无穷多个点是“ 上有无穷多个点是“ 点” 点” |
抛物线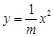 的焦点坐标为( )
的焦点坐标为( )
A.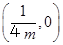 | B.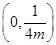 | C.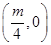 | D.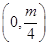 |
抛物线y=x2在点M(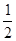 ,
,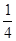 )处的切线的倾斜角是( )
)处的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
若双曲线 的离心率为2,则双曲线
的离心率为2,则双曲线 的离心率为( )
的离心率为( )
A. | B. | C.2 | D. |
斜率为 的直线与双曲线
的直线与双曲线 (a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
A. | B. | C. | D. |
椭圆 的两焦点之间的距离为
的两焦点之间的距离为
A. | B. | C. | D. |
 和
和 为双曲线
为双曲线 (
( )的两个焦点, 若点
)的两个焦点, 若点 和点
和点 是正三角形的三个顶点,则双曲线的离心率为( )。
是正三角形的三个顶点,则双曲线的离心率为( )。


 ,它的一个焦点为F1,则满足
,它的一个焦点为F1,则满足 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )


