题目内容
已知函数f(x)=ln(x-1)-k(x-1)+1。
(1)求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围;
(3)证明: (n∈N*,且n>1)。
(n∈N*,且n>1)。
(1)求函数f(x)的单调区间;
(2)若f(x)≤0恒成立,试确定实数k的取值范围;
(3)证明:
 (n∈N*,且n>1)。
(n∈N*,且n>1)。 解:(1)∵x>1,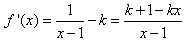 ,
,
1o当k≤0时,f′(x)>0,f(x)在(1,+∞)递增;
2o当k>0时,f(x)在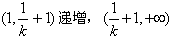 递减;
递减;
(2)当k≤0时,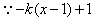 >0(x>1),
>0(x>1),
∴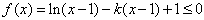 不可能恒成立。
不可能恒成立。
当k>0,由(1)可知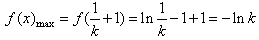 。
。
由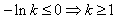 ,
,
∴f(x)≤0恒成立时,k≥1。
(3)构造函数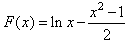 (x>1),
(x>1),
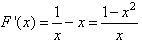 <0,
<0,
∴F(x)在(1,+∞)递减,
∴F(x)<F(1),即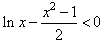 ,
,
∴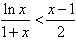 ;
;
当n>1,n∈N*时,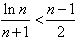 ,
,
∴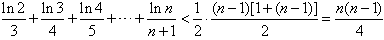 。
。
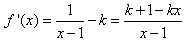 ,
,1o当k≤0时,f′(x)>0,f(x)在(1,+∞)递增;
2o当k>0时,f(x)在
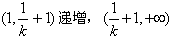 递减;
递减;(2)当k≤0时,
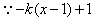 >0(x>1),
>0(x>1),∴
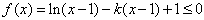 不可能恒成立。
不可能恒成立。 当k>0,由(1)可知
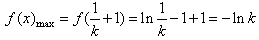 。
。由
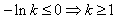 ,
,∴f(x)≤0恒成立时,k≥1。
(3)构造函数
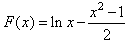 (x>1),
(x>1),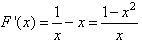 <0,
<0,∴F(x)在(1,+∞)递减,
∴F(x)<F(1),即
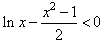 ,
, ∴
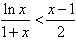 ;
;当n>1,n∈N*时,
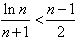 ,
,∴
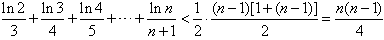 。
。 
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目