题目内容
已知函数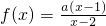 ,a为常数
,a为常数
(1)若f(x)>2的解集为(2,3),求a的值
(2)若f(x)<x-3对任意的x∈(2,+∞)恒成立,求a的取值范围.
解:(1)由解集为(2,3),知x-2>0,即x>2①,
所以f(x)>2即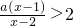 可化为a(x-1)>2(x-2),即(a-2)x>a-4,
可化为a(x-1)>2(x-2),即(a-2)x>a-4,
由解集形式知:a-2<0,所以x< ②,
②,
由①②得2<x< ,
,
所以 =3,解得a=1,;
=3,解得a=1,;
(2)f(x)<x-3即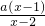 <x-3对任意的x∈(2,+∞)恒成立,等价于a<
<x-3对任意的x∈(2,+∞)恒成立,等价于a<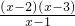 对任意的x∈(2,+∞)恒成立,
对任意的x∈(2,+∞)恒成立,
又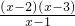 =(x-1)+
=(x-1)+ -3≥2
-3≥2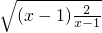 -3=2
-3=2 -3,
-3,
当且仅当x= +1时取等号,
+1时取等号,
所以a<2 -3;
-3;
分析:(1)由解集可知x>2,从而对不等式进行化简,解出不等式后对比解集端点可得关于a的方程,解出即可;
(2)f(x)<x-3对任意的x∈(2,+∞)恒成立,可先分离出参数a后转化为求函数最值解决,对函数进行恰当变形,然后利用基本不等式可求最值;
点评:本题考查函数恒成立问题、根与系数的关系,考查转化思想,考查学生解决问题的能力,解决本题的关键是对问题进行合理转化,变为求函数最值问题.
所以f(x)>2即
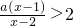 可化为a(x-1)>2(x-2),即(a-2)x>a-4,
可化为a(x-1)>2(x-2),即(a-2)x>a-4,由解集形式知:a-2<0,所以x<
 ②,
②,由①②得2<x<
 ,
,所以
 =3,解得a=1,;
=3,解得a=1,;(2)f(x)<x-3即
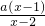 <x-3对任意的x∈(2,+∞)恒成立,等价于a<
<x-3对任意的x∈(2,+∞)恒成立,等价于a<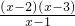 对任意的x∈(2,+∞)恒成立,
对任意的x∈(2,+∞)恒成立,又
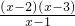 =(x-1)+
=(x-1)+ -3≥2
-3≥2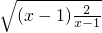 -3=2
-3=2 -3,
-3,当且仅当x=
 +1时取等号,
+1时取等号,所以a<2
 -3;
-3;分析:(1)由解集可知x>2,从而对不等式进行化简,解出不等式后对比解集端点可得关于a的方程,解出即可;
(2)f(x)<x-3对任意的x∈(2,+∞)恒成立,可先分离出参数a后转化为求函数最值解决,对函数进行恰当变形,然后利用基本不等式可求最值;
点评:本题考查函数恒成立问题、根与系数的关系,考查转化思想,考查学生解决问题的能力,解决本题的关键是对问题进行合理转化,变为求函数最值问题.

练习册系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
. 时,求
时,求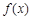 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.