题目内容
某人上午7：00乘汽车以匀速υ1千米/时（30≤υ1≤100）从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以匀速υ2千米/时（4≤υ2≤20）从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地．设乘汽车、摩托车行驶的时间分别是x、y小时，则在xOy坐标系中，满足上述条件的x，y的范围用阴影部分表正确的是（ ）
A、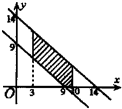 | B、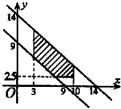 | C、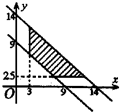 | D、 |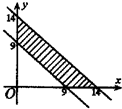
分析：要作出满足条件的x，y的范围，要先分析题意，找出相关量之间的不等关系，即x，y满足的约束条件，由约束条件画出可行域．
解答：
解：依题意得υ2=
，υ1=
，4≤υ2≤20，30≤υ1≤100．
∴3≤x≤10，
≤y≤
．①
由于乘汽车、摩托艇所需的时间和x+y应在9至14个小时之间，即9≤x+y≤14．②
因此，满足①②的点（x，y）的存在范围是图中阴影部分（包括边界）．
故选B．
解：依题意得υ2=| 50 |
| y |
| 300 |
| x |
∴3≤x≤10，
| 5 |
| 2 |
| 25 |
| 2 |
由于乘汽车、摩托艇所需的时间和x+y应在9至14个小时之间，即9≤x+y≤14．②
因此，满足①②的点（x，y）的存在范围是图中阴影部分（包括边界）．
故选B．
点评：在解决线性规划的应用题时，其步骤为：①分析题目中相关量的关系，列出不等式组，即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中．
练习册系列答案
相关题目
