题目内容
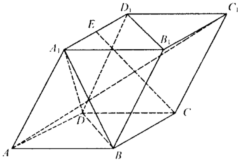（2008•成都三模）已知平行六面体ABCD-A1B1C1D1中，∠A1AD=∠A1AB=∠BAD=60°，AA1=AB=AD，E为A1D1的中点．给出下列四个命题：①∠BCC1为异面直线AD与CC1所成的角；②三棱锥A1-ABD是正三棱锥；③CE⊥平面BB1D1D；④| CE |
| 1 |
| 2 |
| AD |
| AB |
| AA1 |
②④
②④
．（写出所有正确命题的序号）分析：由异面直线所成的角的定义可判断①的真假；利用正三棱锥的定义可判断②的真假；利用直线与平面垂直的定义和向量的数量积运算可判断③的真假；利用向量加法的三角形法则可判断④的真假
解答：解：①∵∠BCC1为120°，而异面直线AD与CC1所成的角为60°，故①错误
②三棱锥A1-ABD的每个面都为正三角形，故为正四面体，故②正确
④根据向量加法的三角形法则，
=
+
+
+
=-
-
+
+
=-
-
+
，故④正确
③∵
=
-
，∴
•
=(-
-
+
)•（
-
）=-
2+
•
-
•
+
2+
•
-
•
=
2-
2+
2-
2=
2≠0
∴CE与BD不垂直，故③错误
故答案为 ②④
②三棱锥A1-ABD的每个面都为正三角形，故为正四面体，故②正确
④根据向量加法的三角形法则，
| CE |
| CB |
| BA |
| AA1 |
| A1E |
| AD |
| AB |
| AA1 |
| 1 |
| 2 |
| A D |
| 1 |
| 2 |
| AD |
| AB |
| AA1 |
③∵
| BD |
| AD |
| AB |
| CE |
| BD |
| 1 |
| 2 |
| AD |
| AB |
| AA1 |
| AD |
| AB |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AD |
| AB |
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
| AB |
| 1 |
| 2 |
| AD |
| 1 |
| 4 |
| AD |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AD |
| 1 |
| 4 |
| AD |
∴CE与BD不垂直，故③错误
故答案为 ②④
点评：本题考查了异面直线所成的角的定义，直线与平面垂直的定义，正三棱锥的定义，向量加法的三角形法则和数量积运算性质
练习册系列答案
阅读快车系列答案
相关题目
（2008•成都三模）如图，已知二面角α-PQ-β的大小为60°，点C为棱PQ一点，A∈β，AC=2，∠ACP=30°，则点A到平面α的距离为（ ）