题目内容
对一切实数x,不等式x2+a|x|+1≥0恒成立,则实数a的取值范围是( )
A.[-2,+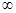 ) ) | B.(-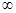 ,-2) ,-2) |
| C.[-2,2] | D.[0,+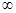 ) ) |
A
解析试题分析: 对一切实数x,恒成立.
对一切实数x,恒成立.
当 时,
时,  恒成立.
恒成立.
当 时,
时, 


因为 的最大值为-2, 故
的最大值为-2, 故
考点:恒成立问题,及参数分离法.

练习册系列答案
相关题目
若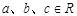 ,且
,且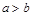 ,则下列不等式中一定成立的是( )
,则下列不等式中一定成立的是( )
A.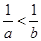 | B.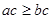 | C.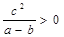 | D.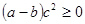 |
设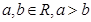 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A. | B.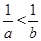 | C. | D.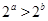 |
已知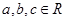 ,给出下列命题:
,给出下列命题:
①若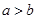 ,则
,则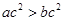 ;②若ab≠0,则
;②若ab≠0,则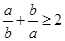 ;③若
;③若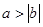 ,则
,则 ;
;
其中真命题的个数为( )
| A.3 | B.2 | C.1 | D.0 |
设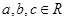 ,且
,且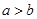 ,则( )
,则( )
A.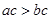 | B.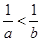 | C.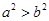 | D.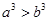 |
若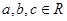 ,且
,且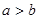 ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )
A.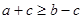 | B.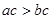 |
C.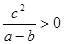 | D.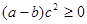 |
已知a>b>1,c<0,给出下列四个结论:
①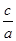 >
>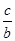 ;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
;②ac<bc;③logb(a-c)>loga(b-c);④ba-c>ab-c.
其中所有正确结论的序号是( )
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
要证明a2+b2-1-a2b2≤0,只要证明( )
| A.2ab-1-a2b2≤0 | B.a2+b2-1- ≤0 ≤0 |
C.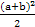 -1-a2b2≤0 -1-a2b2≤0 | D.(a2-1)(b2-1)≥0 |
若x>y>z>1,则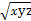 ,
,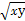 ,
, ,
,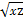 中最大的是( )
中最大的是( )
A.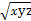 | B.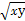 |
C. | D.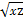 |