题目内容
如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是BB1、D1B1的中点.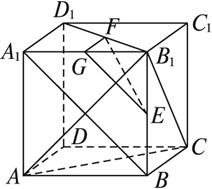
求证:EF⊥平面B1AC.
证明:设A1B1的中点为G,
连结EG、FG、A1B,
则FG∥A1D1,EG∥A1B,
∵A1D1⊥平面A1B.
∴FG⊥平面A1B.
∵A1B⊥AB1,∴EG⊥AB1.
∴EF⊥AB1.
同理,EF⊥B1C.又AB1∩B1C=B1,
∴EF⊥平面B1AC.
练习册系列答案
相关题目
题目内容
如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是BB1、D1B1的中点.
求证:EF⊥平面B1AC.
证明:设A1B1的中点为G,
连结EG、FG、A1B,
则FG∥A1D1,EG∥A1B,
∵A1D1⊥平面A1B.
∴FG⊥平面A1B.
∵A1B⊥AB1,∴EG⊥AB1.
∴EF⊥AB1.
同理,EF⊥B1C.又AB1∩B1C=B1,
∴EF⊥平面B1AC.
如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）