题目内容
函数f(x)=ax3-3x+2a在(1,2)内有最小值,则a的取值范围是______.
【答案】分析:先求出函数的导函数f′(x)=3ax2-3,根据a≤0,f′(x)<0恒成立,函数在(1,2)内无最值,可得a>0,进而根据函数f(x)=ax3-3x+2a在(1,2)内有最小值,可构造关于a的不等式,解不等式可求出a的取值范围
解答:解:∵函数f(x)=ax3-3x+2a
∴f′(x)=3ax2-3
若a≤0,f′(x)=-3<0恒成立
则函数f(x)在(1,2)内无最值
若a>0,令f′(x)=0
则x=±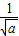
若函数f(x)=ax3-3x+2a在(1,2)内有最小值,则1<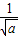 <2,解得
<2,解得 <a<1
<a<1
故答案为: <a<1
<a<1
点评:本题考查的知识点是利用导数研究函数的单调性,其中根据已知构造出关于a的不等式,是解答的关键.
解答:解:∵函数f(x)=ax3-3x+2a
∴f′(x)=3ax2-3
若a≤0,f′(x)=-3<0恒成立
则函数f(x)在(1,2)内无最值
若a>0,令f′(x)=0
则x=±
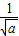
若函数f(x)=ax3-3x+2a在(1,2)内有最小值,则1<
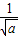 <2,解得
<2,解得 <a<1
<a<1故答案为:
 <a<1
<a<1点评:本题考查的知识点是利用导数研究函数的单调性,其中根据已知构造出关于a的不等式,是解答的关键.

练习册系列答案
相关题目