题目内容
已知函数f(x)=lnx+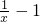
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m∈R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma-(xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2l+1n22+…+ln2n> .
.
解:(Ⅰ)f′(x)= =
= ,x>0.
,x>0.
令f′(x)>0,得x>1,因此函数f(x)的单调递增区间是(1,+∞).
令f′(x)<0,得0<x<1,因此函数f(x)的单调递减区间是(0,1).
(Ⅱ)依题意,ma<f(x)max.
由(Ⅰ)知,f(x)在[1,e]上是增函数,
∴f(x)max=f(e)=lne+ -1=
-1= .
.
∴ma< ,即ma-
,即ma- <0对于任意的a∈(-1,1)恒成立.
<0对于任意的a∈(-1,1)恒成立.
∴ 解得-
解得- ≤m≤
≤m≤ .
.
所以,m的取值范围是[- ,
, ].
].
(Ⅲ)由(Ⅰ)知函数f(x)在[1,+∞)上单调递增,
故f(x)=lnx+ -1≥f(1)=0,
-1≥f(1)=0,
∴lnx≥1- ,以x2替代x,得lnx2≥1-
,以x2替代x,得lnx2≥1- .
.
∴ln2l+1n22+…+ln2n>1- +1-
+1- +…+1-
+…+1-
即ln2l+1n22+…+ln2n>n-( +
+ +…+
+…+ ).
).
又 +
+ +…+
+…+ <1+
<1+ +
+ +…+
+…+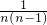
∴-( +
+ +…+
+…+ )>-[1+
)>-[1+ +
+ +…+
+…+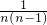 ]
]
∴n-( +
+ +…+
+…+ )>n-[1+
)>n-[1+ +
+ +…+
+…+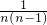 ]=n-[1+1-
]=n-[1+1- +
+ -
- +…+
+…+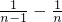 ]=
]= ,
,
∴ln1+ln2+…+lnn> .
.
由柯西不等式,
(ln2l+1n22+…+ln2n)(12+12+…+12)≥(ln1+ln2+…+lnn)2.
∴ln2l+1n22+…+ln2n≥ (ln1+ln2+…+lnn)2>
(ln1+ln2+…+lnn)2> .
.
∴ln2l+1n22,+…+ln2 n> .
.
分析:(I)利用导数求出函数的极值,然后求f(x)的单调区间;
(II)依题意,ma<f(x)max,由(I)可得f(x)在x=e处取得最大值,故问题转化为ma- <0对于任意的a∈(-1,1)恒成立,即可求m的取值范围;
<0对于任意的a∈(-1,1)恒成立,即可求m的取值范围;
(III)由(Ⅰ)知函数f(x)在[1,+∞)上单调递增,从而可得lnx2≥1- .再利用叠加及放缩,可得ln1+ln2+…+lnn>
.再利用叠加及放缩,可得ln1+ln2+…+lnn> 恒成立,再结合柯西不等式即可证明不等式成立.
恒成立,再结合柯西不等式即可证明不等式成立.
点评:本题是中档题,考查函数的导数的应用,不等式的综合应用,柯西不等式的应用,考查计算能力,转化思想的应用.
 =
= ,x>0.
,x>0.令f′(x)>0,得x>1,因此函数f(x)的单调递增区间是(1,+∞).
令f′(x)<0,得0<x<1,因此函数f(x)的单调递减区间是(0,1).
(Ⅱ)依题意,ma<f(x)max.
由(Ⅰ)知,f(x)在[1,e]上是增函数,
∴f(x)max=f(e)=lne+
 -1=
-1= .
.∴ma<
 ,即ma-
,即ma- <0对于任意的a∈(-1,1)恒成立.
<0对于任意的a∈(-1,1)恒成立.∴
 解得-
解得- ≤m≤
≤m≤ .
.所以,m的取值范围是[-
 ,
, ].
].(Ⅲ)由(Ⅰ)知函数f(x)在[1,+∞)上单调递增,
故f(x)=lnx+
 -1≥f(1)=0,
-1≥f(1)=0,∴lnx≥1-
 ,以x2替代x,得lnx2≥1-
,以x2替代x,得lnx2≥1- .
.∴ln2l+1n22+…+ln2n>1-
 +1-
+1- +…+1-
+…+1-
即ln2l+1n22+…+ln2n>n-(
 +
+ +…+
+…+ ).
).又
 +
+ +…+
+…+ <1+
<1+ +
+ +…+
+…+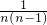
∴-(
 +
+ +…+
+…+ )>-[1+
)>-[1+ +
+ +…+
+…+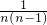 ]
]∴n-(
 +
+ +…+
+…+ )>n-[1+
)>n-[1+ +
+ +…+
+…+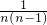 ]=n-[1+1-
]=n-[1+1- +
+ -
- +…+
+…+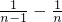 ]=
]= ,
,∴ln1+ln2+…+lnn>
 .
.由柯西不等式,
(ln2l+1n22+…+ln2n)(12+12+…+12)≥(ln1+ln2+…+lnn)2.
∴ln2l+1n22+…+ln2n≥
 (ln1+ln2+…+lnn)2>
(ln1+ln2+…+lnn)2> .
.∴ln2l+1n22,+…+ln2 n>
 .
.分析:(I)利用导数求出函数的极值,然后求f(x)的单调区间;
(II)依题意,ma<f(x)max,由(I)可得f(x)在x=e处取得最大值,故问题转化为ma-
 <0对于任意的a∈(-1,1)恒成立,即可求m的取值范围;
<0对于任意的a∈(-1,1)恒成立,即可求m的取值范围;(III)由(Ⅰ)知函数f(x)在[1,+∞)上单调递增,从而可得lnx2≥1-
 .再利用叠加及放缩,可得ln1+ln2+…+lnn>
.再利用叠加及放缩,可得ln1+ln2+…+lnn> 恒成立,再结合柯西不等式即可证明不等式成立.
恒成立,再结合柯西不等式即可证明不等式成立.点评:本题是中档题,考查函数的导数的应用,不等式的综合应用,柯西不等式的应用,考查计算能力,转化思想的应用.

练习册系列答案
相关题目