题目内容
如果曲线
|
分析:问题可转化为以原点为圆心,以2为半径的圆与圆(x-a)2+(y-a)2=4总相交,根据两圆相交的充要条件两圆心的距离大于0小于2求得a的范围.
解答:解:曲线的方程消去参数得(x-a)2+(y-a)2=4,要使曲线上有且仅有两个点到原点的距离为2,需以原点为圆心,以2为半径的圆与圆(x-a)2+(y-a)2=4总相交,
∴0<
<4?0<a2<8?0<a<2
或-2
<a<0.
故答案为:0<a<2
或-2
<a<0
∴0<
| 2a2 |
| 2 |
| 2 |
故答案为:0<a<2
| 2 |
| 2 |
点评:本题主要考查了直线与圆相交的性质,圆的参数方程以及两圆相交的性质.考查了学生数形结合思想的运用和转化与化归思想的运用.

练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)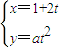 (t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .
(t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .
 (t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .
(t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .