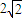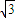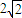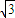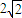题目内容
已知函数f(t)是奇函数且是R上的增函数,若x,y满足不等式f(x2-2x)≤-f(y2-2y),则x2+y2的最大值是
- A.

- B.

- C.8
- D.12
C
分析:先根据函数的单调性和奇偶性把函数问题转化才二元二次不等式,设点P的坐标为(x,y),进而根据不等式的形式判断点P是以(1,1)为圆心, 为半径的圆上及以内的点,进而根据图象可知
为半径的圆上及以内的点,进而根据图象可知 的最大值为圆的直径,进而求得x2+y2的最大值.
的最大值为圆的直径,进而求得x2+y2的最大值.
解答:∵f(x2-2x)≤-f(y2-2y),
∴f(x2-2x)≤f(-y2+2y),
∵f(x)是增函数
∴x2-2x≤-y2+2y,整理得(x-1)2+(y-1)2≤2
设点P的坐标为(x,y)则点P是以(1,1)为圆心, 为半径的圆上及以内的点,而此圆过原点
为半径的圆上及以内的点,而此圆过原点
则 为点P到原点的距离,
为点P到原点的距离,
∵圆过原点,
∴ 的最大值为圆的直径2
的最大值为圆的直径2
∴x2+y2的最大值为8
故选C
点评:本题主要考查了函数的奇偶性的应用及解不等式的问题.解题的关键是根据不等式的形式利用数形结合的方法直观的解决问题.
分析:先根据函数的单调性和奇偶性把函数问题转化才二元二次不等式,设点P的坐标为(x,y),进而根据不等式的形式判断点P是以(1,1)为圆心,
 为半径的圆上及以内的点,进而根据图象可知
为半径的圆上及以内的点,进而根据图象可知 的最大值为圆的直径,进而求得x2+y2的最大值.
的最大值为圆的直径,进而求得x2+y2的最大值.解答:∵f(x2-2x)≤-f(y2-2y),
∴f(x2-2x)≤f(-y2+2y),
∵f(x)是增函数
∴x2-2x≤-y2+2y,整理得(x-1)2+(y-1)2≤2
设点P的坐标为(x,y)则点P是以(1,1)为圆心,
 为半径的圆上及以内的点,而此圆过原点
为半径的圆上及以内的点,而此圆过原点则
 为点P到原点的距离,
为点P到原点的距离,∵圆过原点,
∴
 的最大值为圆的直径2
的最大值为圆的直径2
∴x2+y2的最大值为8
故选C
点评:本题主要考查了函数的奇偶性的应用及解不等式的问题.解题的关键是根据不等式的形式利用数形结合的方法直观的解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目