题目内容
(2007•温州一模)设直线y=x+1与抛物线x2=4y交于A、B两点,则AB的中点到x轴的距离为
3
3
.分析:根据题意可设A(x1,y1),B(x2,y2),C(x0,y0),可得C到x轴的距离为 y0=
,再联立直线与抛物线的方程结合根与系数的关系即可得到答案.
| y1+y2 |
| 2 |
解答: 解:由题意可得如图所示:
解:由题意可得如图所示:
设A(x1,y1),B(x2,y2),AB的中点C(x0,y0)
因为C为AB的中点,所以 y0=
,
所以C到x轴的距离为 y0=
.
联立直线与抛物线的方程
,消去x,
可得:y2-6y+1=0,
所以由根与系数的关系可得
y1+y2=6,
∴y0=
=3.
则AB的中点到x轴的距离为 3
故答案为:3.
 解:由题意可得如图所示:
解:由题意可得如图所示:设A(x1,y1),B(x2,y2),AB的中点C(x0,y0)
因为C为AB的中点,所以 y0=
| y1+y2 |
| 2 |
所以C到x轴的距离为 y0=
| y1+y2 |
| 2 |
联立直线与抛物线的方程
|
可得:y2-6y+1=0,
所以由根与系数的关系可得
y1+y2=6,
∴y0=
| y1+y2 |
| 2 |
则AB的中点到x轴的距离为 3
故答案为:3.
点评:本题的考点是直线与抛物线的关系,解决此类问题的关键是熟练掌握抛物线与直线的位置关系,以及方程思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
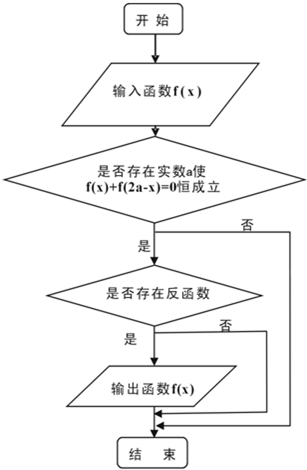 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )