题目内容
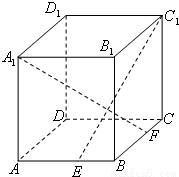
19.如图,ABCD—A1B
(Ⅰ)求三棱锥D1—DBC的体积;
(Ⅱ)证明BD1∥平面C1DE;
(Ⅲ)求面C1DE与面CDE所成二面角的正切值.
19.
(Ⅰ)解:![]() =
=![]() ·
·![]() ·2·2·1=
·2·2·1=![]() .
.
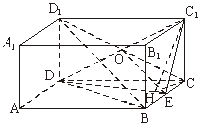
(Ⅱ)证明:记D
∵O是CD1的中点,E是BC的中点,
∴EO∥BD1.
∵BD1![]() 平面C1DE,EO
平面C1DE,EO![]() 平面C1DE,
平面C1DE,
∴BD1∥平面C1DE.
(Ⅲ)解:过C作CH⊥DE于H,连结C1H.
在正四棱柱ABCD—A1B
∴C1H⊥DE,
∴∠C1HC是面C1DE与面CDE所成二面角的平面角.
∵DC=2,CC1=1,CE=1,
∴CH=![]() ,
,
∴tanC1HC=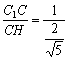 =
=![]() .
.
即面C1DE与面CDE所成二面角的正切值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
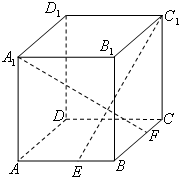 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是