题目内容
三个共面且不共线向量
，
，
两两所成的角相等，且|
|=1，|
|=2，|
|=3，则|
+
+
|等于（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
分析：由题意可得
、
、
两两所成的角都等于120°，根据向量数量积的公式算出
•
=-1、
•
=-3、
•
=-
，从而算出（
+
+
）2=3，利用向量模的公式即可算出|
+
+
|的值．
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| 3 |
| 2 |
| a |
| b |
| c |
| a |
| b |
| c |
解答：解：∵向量
、
、
两两所成的角相等，且不共线，
∴
、
、
两两所成的角都等于120°．
∵|
|=1，|
|=2，|
|=3，
∴
•
=|
|•|
|cos120°=-1，
•
=|
|•|
|cos120°=-3，
•
=|
|•|
|cos120°=-
．
由此可得（
+
+
）2=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
=1+4+9-2-6-3=3，
∴|
+
+
|=
=
．
故选：A
| a |
| b |
| c |
∴
| a |
| b |
| c |
∵|
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
| b |
| c |
| b |
| c |
| a |
| c |
| a |
| c |
| 3 |
| 2 |
由此可得（
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
∴|
| a |
| b |
| c |
(
|
| 3 |
故选：A
点评：本题给出两两夹角相等的三个向量，在已知它们的模的情况下求它们的和向量的模．着重考查了向量数量积的公式和向量模的公式等知识，属于中档题．
练习册系列答案
相关题目
满足：
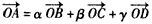(α，β，γ∈R)，B、C、D为不共线的三个点，给出下列命题：
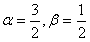，γ=-1，则A、B、C、D四点共面；
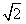时，若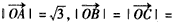
，
，
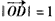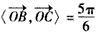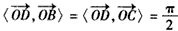，则α+β的最大值是
；
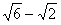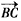所成的比A一定为
；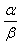