题目内容
设a，b，c，d，m，n都是正实数，P=
+
，Q=
•
，则P与Q的大小
| ab |
| cd |
| ma+nc |
|
P≤Q
P≤Q
．分析：由题知，此两式皆为根式，可先比较两者的平方，通过两者平方的大小得出两数的大小
解答：解：由题意P2=ab+cd+2
，
Q2=ab+cd+
+
≥ab+cd+2
，
所以P2≥Q2，即P≥Q
故答案为P≥Q
| abcd |
Q2=ab+cd+
| nbc |
| m |
| mad |
| n |
| abcd |
所以P2≥Q2，即P≥Q
故答案为P≥Q
点评：本题考查基本不等式比较大小，解答的关键是平方转化，通过比较平方的大小来比较两数大小，本题考查了转化的思想
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
+
,Q=
,则有( )
+
,q=
·
，那么( )
+
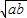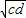，Q=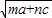
•
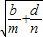，则有（ ）