Question

在等差数列{a_n}中,已知a₅=10,a₁₂=31,求数列{a_n}的通项公式.

Answer 1

解法一:由题意知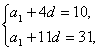,解得?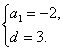

∴a_n=a₁+(n-1)d=-2+(n-1)·3=3n-5.

解法二:因为等差数列的通项公式是关于正自然数n的一次函数，故设a_n=a.n+b，则解得a=3,b=-5,所以a_n=3n-5.

解法三:因为a₁₂=a₅+7d,则31=10-7d,解得d=3,又a_n=a₅+(n-5)d=10+(n-5)3=3n-5.