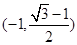题目内容
函数 的值域是
的值域是
- A.[-4,0)
- B.[-4,4)
- C.(-4,0]
- D.[-4,0]
C
分析:利用和差化积公式化简函数 后,根据正弦函数的有界性求出函数的值域.
后,根据正弦函数的有界性求出函数的值域.
解答:y= =-
=- =-4sin2x(cosx≠0)
=-4sin2x(cosx≠0)
即sinx≠±1
因为 0≤sin2x≤1 且sinx≠±1
所以 0≤sin2x<1
所以函数 的值域是:(-4,0]
的值域是:(-4,0]
故选C
点评:本题考查三角函数的恒等变形,和差化积公式的应用,注意正弦函数的值域,余弦函数的值域这一隐含条件的挖掘,是解好题目的注意点.
分析:利用和差化积公式化简函数
 后,根据正弦函数的有界性求出函数的值域.
后,根据正弦函数的有界性求出函数的值域.解答:y=
 =-
=- =-4sin2x(cosx≠0)
=-4sin2x(cosx≠0)即sinx≠±1
因为 0≤sin2x≤1 且sinx≠±1
所以 0≤sin2x<1
所以函数
 的值域是:(-4,0]
的值域是:(-4,0]故选C
点评:本题考查三角函数的恒等变形,和差化积公式的应用,注意正弦函数的值域,余弦函数的值域这一隐含条件的挖掘,是解好题目的注意点.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 ,则函数
,则函数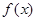 的值域是( ).
的值域是( ).  B.
B.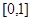 C.
C.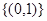 D.
D.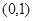
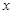 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数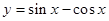 的值域是( )
的值域是( ) B.
B.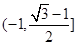 C.
C.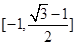 D.
D.